旋转图像（48）

PNG

今天是小浩算法 “365刷题计划” 第103天。这是前几天一个同学去滴滴面试的原题。

01、题目示例

这道题目和昨天讲的生命游戏有一点是很像的，就是同样也要求原地旋转。其实在很多矩阵的题目中，都会有这样的要求，大家需要注意一下。

第48题：旋转图像
给定一个 n × n 的二维矩阵表示一个图像。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。


示例 1:

  1. 给定 matrix = 
  2. [
  3.   [1,2,3],
  4.   [4,5,6],
  5.   [7,8,9]
  6. ],
  8. 原地旋转输入矩阵，使其变为:
  9. [
  10.   [7,4,1],
  11.   [8,5,2],
  12.   [9,6,3]
  13. ]

示例 2:

  1. 给定 matrix =
  2. [
  3.   [ 5, 1, 9,11],
  4.   [ 2, 4, 8,10],
  5.   [13, 3, 6, 7],
  6.   [15,14,12,16]
  7. ], 
  9. 原地旋转输入矩阵，使其变为:
  10. [
  11.   [15,13, 2, 5],
  12.   [14, 3, 4, 1],
  13.   [12, 6, 8, 9],
  14.   [16, 7,10,11]
  15. ]

题目理解起来还是很容易的：

PNG

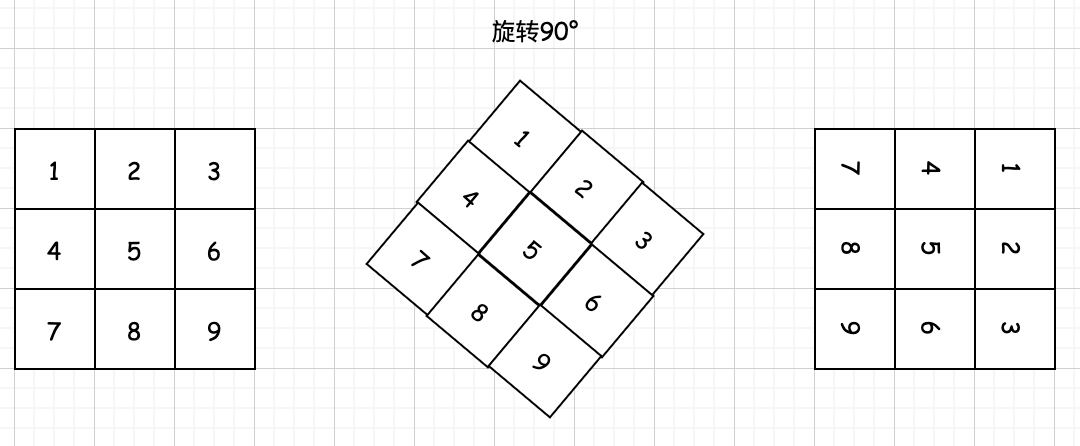
02、题解分析

这是一道看起来容易，但其实非常考察细心程度的算法题目，有太多地方会出现失误。


我们用代码来旋转矩阵，肯定不能说像拿着一个东西整体直接旋转，类似这样：

PNG

一般容易想到的是，一层层的从外到内旋转每一圈（至于为什么不从内到外，如果你觉得方便，也ok），也就是俗称的找框框：

PNG

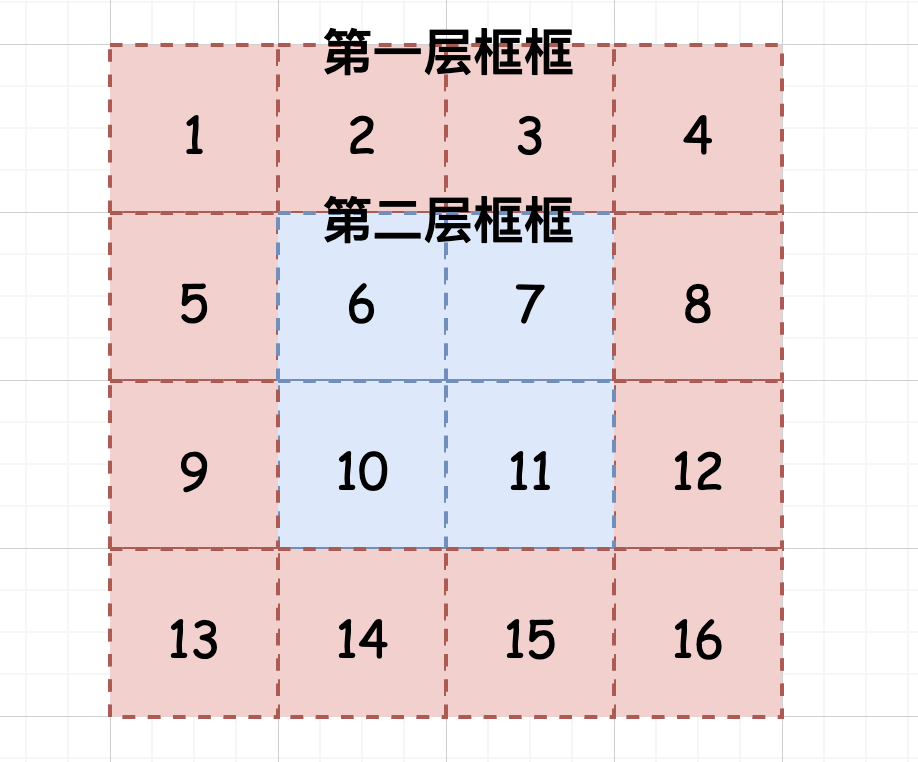
对每个框框，其实都有 4 个顶点：

PNG

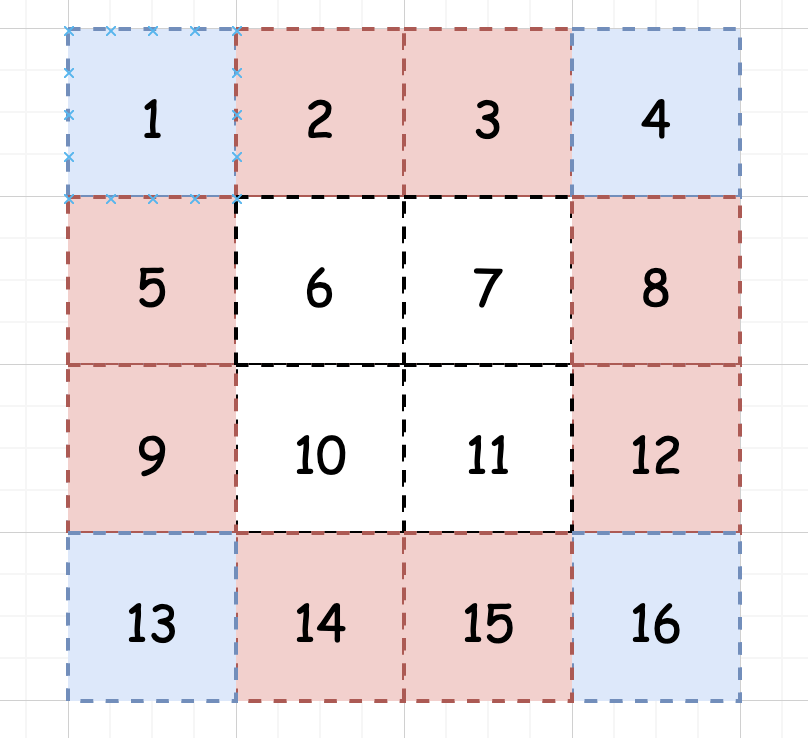
剩下的就是交换这四个顶点的值：

PNG

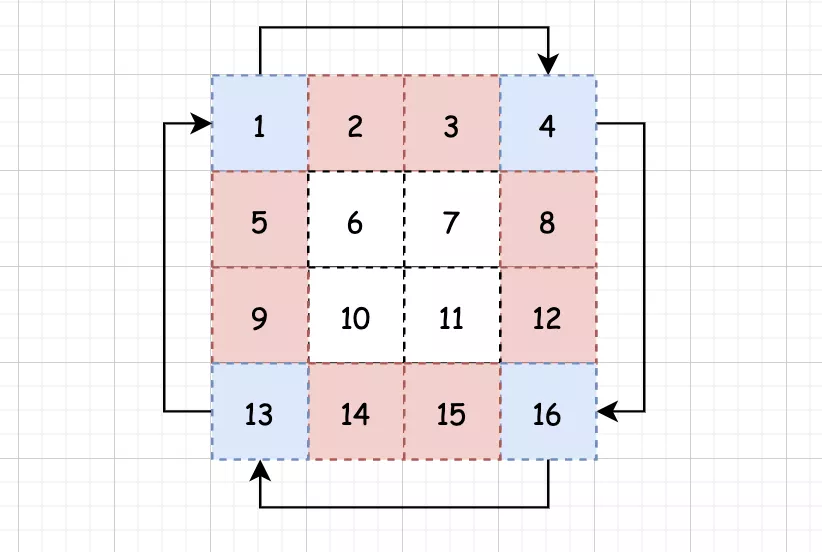
交换完毕之后，再继续交换移动后的四个顶点：

PNG

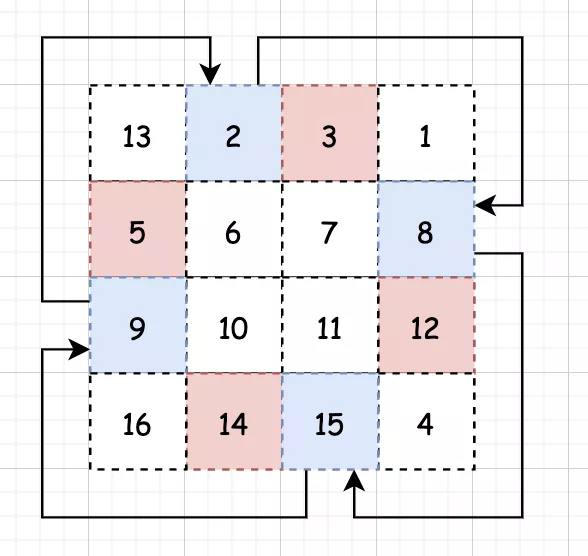
那代码实现其实就很简单了：


  • 我们通过 x 和 y 就可以定义这个框框的边界
  • 找到框框后，我们再通过框框边界来定义出4个顶点
  • 然后完成交换
  1. //java
  2. class Solution {
  3.     public void rotate(int[][] matrix) {
  4.         int temp;
  5.         for (int x = 0, y = matrix[0].length - 1; x < y; x++, y--) {
  6.             for (int s = x, e = y; s < y; s++, e--) {
  7.                 temp = matrix[x][s];
  8.                 matrix[x][s] = matrix[e][x];
  9.                 matrix[e][x] = matrix[y][e];
  10.                 matrix[y][e] = matrix[s][y];
  11.                 matrix[s][y] = temp;
  12.             };
  13.         };
  14.     }
  15. }

当然，上面是一个 n x n 的矩阵找框框，如果不是 n x n 其实也类似，大家有兴趣可以看下下面这道：

螺旋矩阵（54）


那我们除了找框框之外，还能不能有一些别的解法呢？当然可以，想想小时候我们通过对折来完成的填字游戏。

PNG

我们观察这个矩阵：

PNG

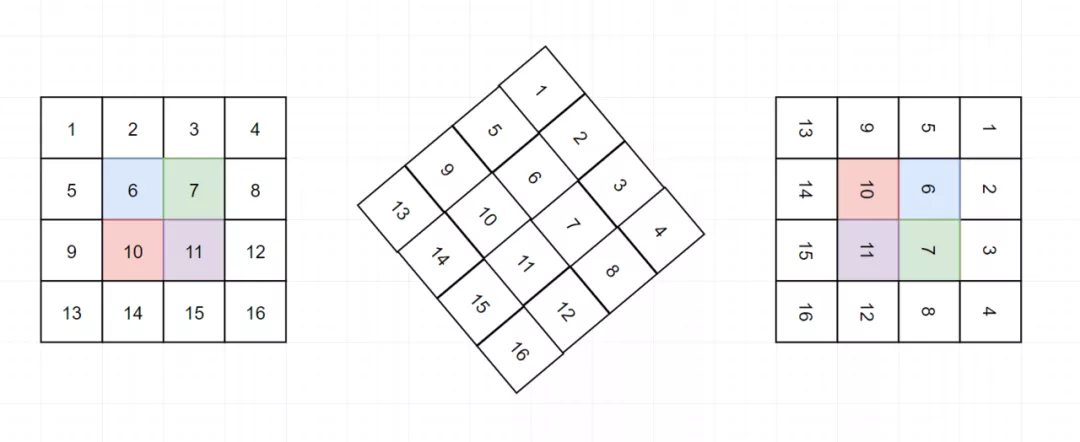
我们观察这个矩阵，向右旋转90°，是不是可以理解为先上下翻转，再沿对角线翻转：

PNG

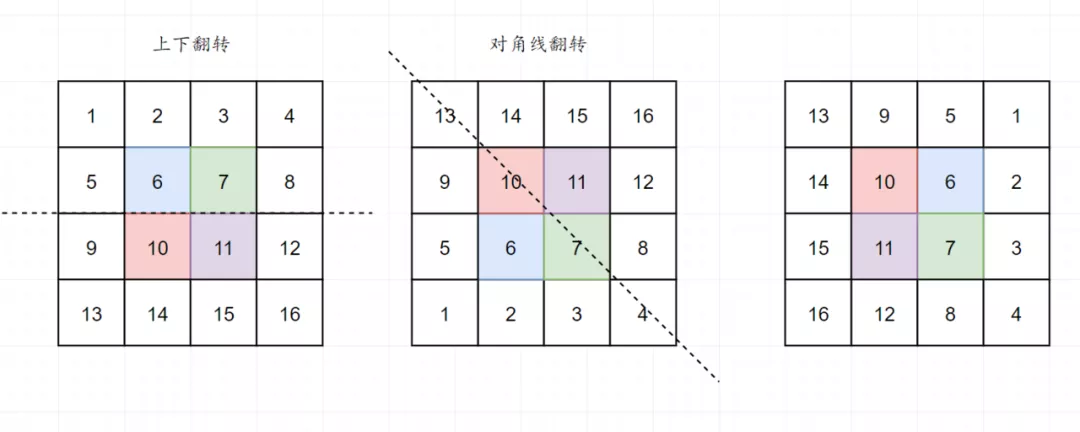
根据分析，完成代码（其实应该用Go写，交换元素会方便许多….）：

  1. //JAVA
  2. class Solution {    
  3.     public void rotate(int[][] matrix) {        
  4.         int n = matrix.length;        
  5.         //上下翻转        
  6.         for (int i = 0; i < n / 2; i ++){            
  7.             int[] tmp = matrix[i];            
  8.             matrix[i] = matrix[n - i - 1];            
  9.             matrix[n - i - 1] = tmp;       
  10.         }        
  11.         //对角线翻转        
  12.         for (int i = 0; i < n; i ++){            
  13.             for (int j= i + 1; j < n; j++){                
  14.                 int tmp = matrix[i][j];                
  15.                 matrix[i][j] = matrix[j][i];                
  16.                 matrix[j][i] = tmp;            
  17.             }       
  18.         }    
  19.     }
  20. }

执行结果：

PNG

03、算法小知识

骑士巡逻（英语：Knight’s tour）是指在按照国际象棋中骑士的规定走法走遍整个棋盘的每一个方格，而且每个网格只能够经过一次。假若骑士能够从走回到最初位置，则称此巡逻为“封闭巡逻”，否则，称为“开巡逻”。对于8*8棋盘，一共有26,534,728,821,064种封闭巡逻，但是到底有多少种开巡逻仍然未知。

PNG

PNG


今天的题目到这里就结束了，你学会了吗？快来评论区留下你的想法吧！