第k个最大元素（215）

今天给大家分享一道美团面试题。话不多说，直接看题。

01、题目示例

这个题目的变形很多，比如找 “前 K 个高频元素”、 “数据流中的第K大元素” 、”最接近原点的 K 个值” 等等等等。

第215题：第K个最大元素
在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

  1. 输入: [3,2,1,5,6,4] 和 k = 2
  2. 输出: 5

示例 2:

  1. 输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
  2. 输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。


02、大顶堆

堆在算法题目中的应用主要包括以下几点：

  • TopK 问题 （尤其是大数据处理）
  • 优先队列
  • 利用堆求中位数


这种题目，从个人来讲，我一般是比较偏好使用堆来做的。毕竟大小顶堆，刚好有着与本类题型契合的特性。如果对堆不太熟悉的话，可以先看下这篇文章：

那本题如何使用堆来做呢？假若我们的数组为[3,2,1,5,6,4]，k=2，我们对其构造一个小顶堆（每个结点的值均不大于其左右孩子结点的值，堆顶元素为整个堆的最小值），整个过程是这样：


  • 构造一个小顶堆，依次将元素放入堆中，并保证堆中元素为k。

    PNG

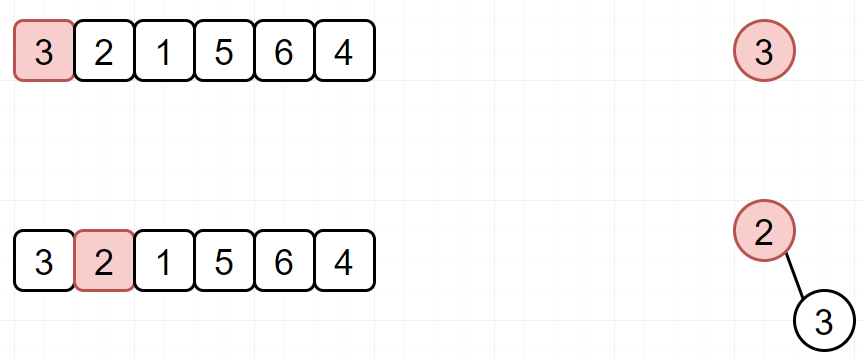
  • 如果当前元素小于堆顶元素，那基本就不用看了（因为我们要找的是 排序后的第 k 个最大的元素）

    PNG

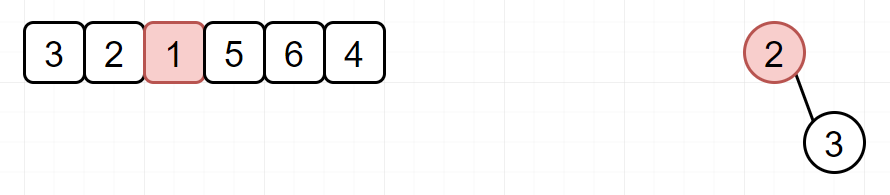
  • 自然，如果我们遇到比堆顶元素大的元素，就把它放入到堆中。

    PNG

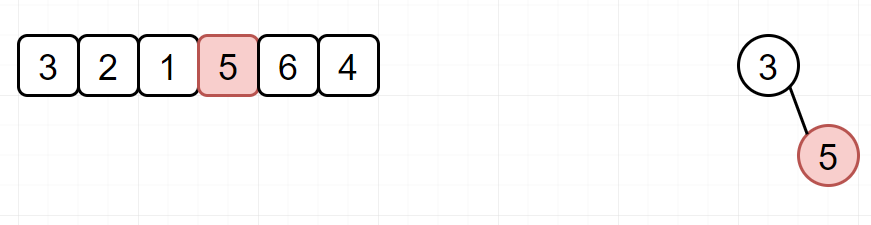
  • 重复上面的步骤：

    PNG

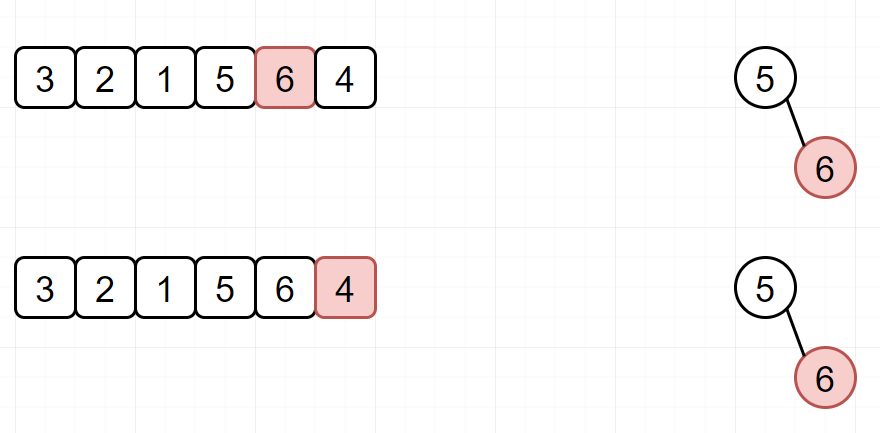
然后根据分析，完成代码（今天就不手撕堆了，因为之前已经手撕过了。同时这里给大家一个建议，如果面试的时候，遇到这种TOPK的问题，假如特别有把握，肯定得手撕数据结构，一定会加分。但是如果没有把握，那就先用API实现，以 BugFree 为目标吧！）

  1. //java
  2. class Solution {
  3.     public int findKthLargest(int[] nums, int k) {
  4.         PriorityQueue<Integer> minQueue = new PriorityQueue<>(k);
  5.         for (int num : nums) {
  6.             if (minQueue.size() < k || num > minQueue.peek()) {
  7.                 minQueue.offer(num);
  8.             }
  9.             if (minQueue.size() > k) {
  10.                 minQueue.poll();
  11.             }
  12.         }
  13.         return minQueue.peek();
  14.     }
  15. }

我也不知道为啥，Python永远就是这么牛X，朴实无华且枯燥！

  1. //python
  2. class Solution:
  3.     def findKthLargest(self, nums: List[int], k: int) -> int:
  4.         return heapq.nlargest(k, nums)[-1] # [6,5]

注：python可以使用heapq.nlargest 或 heapq.nsmallest，来找出某个集合中找出最大或最小的N个元素。

  1. //python
  2. >>> import heapq
  3. >>> nums=[1,8,2,23,7,-4,18,23,42,37,2]
  4. >>> print(heapq.nlargest(3,nums))
  5. [42, 37, 23]
  6. >>> print(heapq.nsmallest(3,nums))
  7. [-4, 1, 2]

03、快排

快速排序（Quicksort）是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1960年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。


那对于本题，我们就是使用快排的思想，选定一个基准值，把比基准值大的放在基准值的右边，把基准值小的放在基准值的左边。若基准值刚好位于倒数第k个数，则基准值为目标值；反之，则递归处理目标值所处的那一部分数组。

  1. func findKthLargest(nums []int, k int) int {
  2.     idx := quickSort(0, len(nums) - 1, len(nums) - k, nums)
  3.     return nums[idx]
  4. }
  6. func quickSort(l, r, pos int, nums []int) int {
  7.     povit_idx := partition(l, r, nums)
  8.     if pos == povit_idx {
  9.         return povit_idx
  10.     } else if pos > povit_idx {
  11.         return quickSort(povit_idx + 1, r, pos, nums)
  12.     } else {
  13.         return quickSort(l, povit_idx - 1, pos, nums)
  14.     }
  15. }
  17. func partition(l, r int, nums []int) int {
  18.     s := l
  19.     povit_value := nums[l]
  20.     for l < r {
  21.         for ;l < r && nums[r] >= povit_value; {
  22.             r--
  23.         }
  24.         for ;l < r && nums[l] <= povit_value; {
  25.             l++
  26.         }
  27.         if l < r {
  28.             nums[l] = nums[r] ^ nums[l]
  29.             nums[r] = nums[l] ^ nums[r]
  30.             nums[l] = nums[r] ^ nums[l]
  31.         }
  32.     }
  33.     nums[s] = nums[l]
  34.     nums[l] = povit_value
  35.     return l
  36. }

执行结果：

PNG

整个快排的核心，其实就partition。partition 有 单向扫描，双向扫描 等多种写法。上面的代码，大家可以参考参考，看不懂也没关系，我后面是会单独安排一个快排的系列篇来进行讲解的，到时候一堆图解砸进来，保准你看的醍醐灌顶！


所以，今天的问题你学会了吗？评论区留下你的想法！