伪蒙特卡洛
分享一道由群员“Melbourne”,外号 “Paper Machine”,有数学小王子之称的小伙伴分享的题目!
特别说明:本文非原创,经投稿者同意后发表。
01、算法介绍
期望:在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
| 题目:在1*1的正方形中随机撒三个点,两两点都可构成长方形的一组对顶点,这样一共有三个长方形,需要求面积第二大的长方形的面积的期望。 |
|---|
| 算法:每次随机三个点,计算第二大面积,最后统计期望。 |
02、蒙特卡洛
蒙特卡罗法也称统计模拟法、统计试验法。是把概率现象作为研究对象的数值模拟方法。是按抽样调查法求取统计值来推定未知特性量的计算方法。蒙特卡罗是摩纳哥的著名赌城,该法为表明其随机抽样的本质而命名。故适用于对离散系统进行计算仿真试验。在计算仿真中,通过构造一个和系统性能相近似的概率模型,并在数字计算机上进行随机试验,可以模拟系统的随机特性。
蒙特卡洛方法(Monte Carlo Method) 指的是一类使用随机变量解决概率问题的方法。比较常见的是计算积分、计算概率、计算期望等问题。
常见的蒙特卡洛方法依赖于随机变量的“随机性”,即未发生的事件无法根据已有信息进行预测,比如抛硬币、掷骰子等。在计算机中,常见的随机数是由一系列确定性算法进行生成的,通常称之为伪随机数(pseudo random number)。由于计算精度有限,且这些随机数在统计意义上“不够随机”,会出现可预测的重复序列,这些数在统计意义上收敛精度有限。
与常见的蒙特卡洛方法不同的是,伪蒙特卡洛使用了低差异序列(low discrepancy sequence,常见的有halton序列、sobol序列等),不使用常见的(伪)随机数,其收敛速率更快(记 N 为样本数量,伪蒙特卡洛收敛速率可达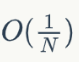 ,而普通蒙特卡洛方法收敛速率仅为
,而普通蒙特卡洛方法收敛速率仅为 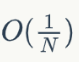 。另一个最重要的性质是伪蒙特卡洛使用的低差异序列是可复现的(replicable),即不会随环境改变而改变,没有随机种子;而普通蒙特卡洛使用的伪随机数会因随机种子不同而导致结果不同,收敛效果也不尽相同。
。另一个最重要的性质是伪蒙特卡洛使用的低差异序列是可复现的(replicable),即不会随环境改变而改变,没有随机种子;而普通蒙特卡洛使用的伪随机数会因随机种子不同而导致结果不同,收敛效果也不尽相同。
03、题目分析
本算法利用伪蒙特卡洛完成。
CPP代码如下:
#include <cmath>#include <cstdio>#include <vector>#include <cassert>#include <omp.h>const int UP=100;bool sieve[UP 100];int primes[UP],top=0;void init(){for (int i=2;i<=UP; i)if (!sieve[i]){primes[top ]=i;for (int j=i;j<=UP/i; j)sieve[i*j]=true;}}std::vector<double> halton(long long i,const int &dim){assert(dim<=top);std::vector<double> prime_inv(dim,0),r(dim,0);std::vector<long long> t(dim,i);for (int j=0;j<dim; j)prime_inv[j]=1.0/primes[j];auto f=[](const std::vector<long long> &t)->long long {long long ret=0;for (const auto &e:t)ret =e;return ret;};for (;f(t)>0;)for (int j=0;j<dim; j){long long d=t[j]%primes[j];r[j] =d*prime_inv[j];prime_inv[j]/=primes[j];t[j]/=primes[j];}return r;}double experiment(long long idx){std::vector<double> li=halton(idx,6);double area1=fabs((li.at(0)-li.at(2))*(li.at(1)-li.at(3)));double area2=fabs((li.at(0)-li.at(4))*(li.at(1)-li.at(5)));double area3=fabs((li.at(2)-li.at(4))*(li.at(3)-li.at(5)));double w=area1 area2 area3-std::max(std::max(area1,area2),area3)-std::min(std::min(area1,area2),area3);return w;}const int BATCH=100000;const int THREADS=40;int main(){init();double total=0;for (long long trial=0;;){std::vector<double> li(THREADS,0);omp_set_dynamic(0);omp_set_num_threads(THREADS);#pragma omp parallel forfor (long long thread=0;thread<THREADS; thread){for (long long i=0;i<BATCH; i)li.at(thread) =experiment(trial thread*BATCH i);}for (const auto &d:li)total =d;trial =THREADS*BATCH;printf("%lld: %.10f\n",trial,total/trial),fflush(stdout);}return 0;}
分析:使用了并行计算,批量跑随机实验,速度大大提升。其中halton函数会生成halton低差异序列,其值域为[0,1],参数i表示第i个抽样,dim表示生成数据的维度(本例中每次实验需要6个点,使用6维数据点即可),不同样本之间互不影响,故可使用并行计算提速。
#表示随机试验次数×10^7,Avg表示第二大面积的平均值,Err表示与真实值的绝对误差×10^(-10)。
| # | Avg | Err | # | Avg | Err |
|---|---|---|---|---|---|
| 1 | 0.1017786804 | 55 | 2 | 0.1017786707 | 152 |
| 3 | 0.1017786905 | 46 | 4 | 0.1017786889 | 30 |
| 5 | 0.1017786809 | 50 | 6 | 0.1017786836 | 23 |
| 7 | 0.1017786849 | 10 | 8 | 0.1017786868 | 9 |
| 9 | 0.1017786799 | 60 | 10 | 0.1017786837 | 22 |
| 11 | 0.1017786845 | 14 | 12 | 0.1017786839 | 20 |
| 13 | 0.1017786874 | 15 | 14 | 0.1017786839 | 20 |
| 15 | 0.1017786848 | 11 | 16 | 0.1017786868 | 9 |
| 17 | 0.1017786851 | 8 | 18 | 0.1017786863 | 4 |
| 19 | 0.1017786854 | 5 | 20 | 0.1017786887 | 28 |
| 21 | 0.1017786858 | 1 | 22 | 0.1017786844 | 15 |
| 23 | 0.1017786841 | 18 | 24 | 0.1017786852 | 7 |
| 25 | 0.1017786849 | 10 | 26 | 0.101778684 | 19 |
| 27 | 0.1017786838 | 21 | 28 | 0.1017786852 | 7 |
| 29 | 0.1017786838 | 21 | 30 | 0.1017786846 | 13 |
| 31 | 0.1017786859 | 0 | 32 | 0.1017786862 | 3 |
| 33 | 0.1017786859 | 0 | 34 | 0.1017786853 | 6 |
| 35 | 0.1017786854 | 5 | 36 | 0.1017786859 | 0 |
| 37 | 0.101778685 | 9 | 38 | 0.1017786854 | 5 |
| 39 | 0.1017786853 | 6 | 40 | 0.1017786858 | 1 |
| 41 | 0.1017786848 | 11 | 42 | 0.1017786851 | 8 |
| 43 | 0.1017786847 | 12 | 44 | 0.1017786841 | 18 |
| 45 | 0.101778685 | 9 | 46 | 0.1017786842 | 17 |
| 47 | 0.1017786852 | 7 | 48 | 0.1017786848 | 11 |
| 49 | 0.1017786854 | 5 | 50 | 0.1017786851 | 8 |
| 51 | 0.1017786842 | 17 | 52 | 0.1017786844 | 15 |
可以看到,在实验次之后,收敛精度可达9位小数,非常精确。由于使用的随机数“不够随机”,普通的蒙特卡洛在同样的实验次数下仅能收敛至五位小数的精度。
上述方法可扩展至其他随机问题中,非常实用且高效,欢迎大家讨论!
所以,今天的问题你学会了吗?评论区留下你的想法!
