平衡二叉树(110)

在之前的系列中，我们已经学习了二叉树的深度以及DFS，如果不会可以先查看之前的文章。今天我们将对其进行应用，直接看题目。

01、题目分析

第110题：平衡二叉树
给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。


示例 1:

  1. 给定二叉树 [3,9,20,null,null,15,7]
  3.     3
  4.    / \
  5.   9  20
  6.     /  \
  7.    15   7 
  9. 返回 true 。

示例 2:

  1. 给定二叉树 [1,2,2,3,3,null,null,4,4]
  3.        1
  4.       / \
  5.      2   2
  6.     / \
  7.    3   3
  8.   / \
  9.  4   4
  11. 返回 false 。

02、图解分析

首先分析题目，这道题思路很简单，我们想判断一棵树是否满足平衡二叉树，无非就是判断当前结点的两个孩子是否满足平衡，同时两个孩子的高度差是否超过1。那只要我们可以得到高度，再基于高度进行判断即可。


我们先复习一下之前对于树高度的求解：

img

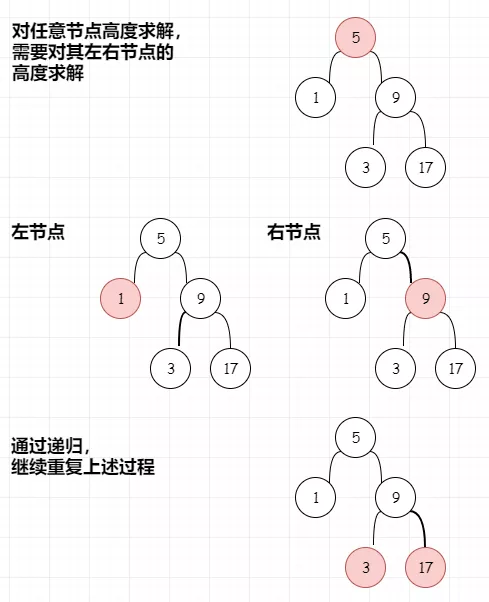
这里唯一要注意的是，当我们判定其中任意一个节点如果不满足平衡二叉树时，那说明整棵树已经不是一颗平衡二叉树，我们可以对其进行阻断，不需要继续递归下去。


另外，需要注意的是，下面这棵并不是平衡二叉树：

img

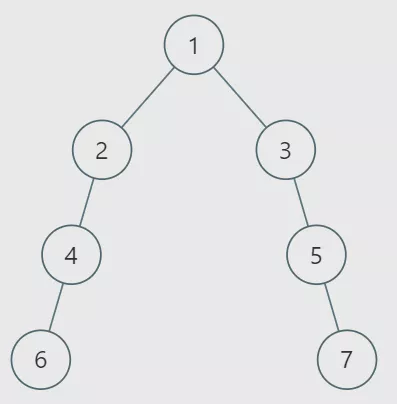
03、代码分析

根据分析，逻辑非常清晰，顺利得出代码：

  1. func isBalanced(root *TreeNode) bool {
  2.     if root == nil {
  3.         return true
  4.     }
  5.     if !isBalanced(root.Left) || !isBalanced(root.Right) {
  6.         return false
  7.     }
  8.     leftH := maxDepth(root.Left) + 1;     
  9.     rightH := maxDepth(root.Right) + 1;   
  10.     if abs(leftH-rightH) > 1 {
  11.         return false
  12.     }
  13.     return true
  14. }
  16. func maxDepth(root *TreeNode) int {
  17.     if root == nil {
  18.         return 0
  19.     }
  20.     return max(maxDepth(root.Left),maxDepth(root.Right)) + 1
  21. }
  23. func max(a,b int) int {
  24.     if a > b {
  25.         return a
  26.     }
  27.     return b
  28. }
  30. func abs(a int) int {
  31.     if a < 0 {
  32.         return -a
  33.     }
  34.     return a 
  35. }

执行结果：

img