二叉树的剪枝(814)

在之前的系列中。我们学习了DFS、BFS，也熟悉了平衡二叉树，满二叉树，完全二叉树，BST（二叉搜索树）等概念。在本节中，我们将学习一种二叉树中常用的操作 —剪枝。这里额外说一点，就本人而言，对这个操作以及其衍化形式的使用会比较频繁。因为我是做规则引擎的，在规则引擎中，我们会有一个概念叫做决策树，那如果一颗决策树完全生长，就会带来比较大的过拟合问题。因为完全生长的决策树，每个节点只会包含一个样本。所以我们就需要对决策树进行剪枝操作，来提升整个决策模型的泛化能力（ML概念）… 听不懂也没关系，简单点讲，就是我觉得这个很重要，或者每道算法题都很重要。如果你在工作中没有用到，不是说明算法不重要，而可能是你还不够重要。

01、剪枝概述

假设有一棵树，最上层的是root节点，而父节点会依赖子节点。如果现在有一些节点已经标记为无效，我们要删除这些无效节点。如果无效节点的依赖的节点还有效，那么不应该删除，如果无效节点和它的子节点都无效，则可以删除。剪掉这些节点的过程，称为剪枝，目的是用来处理二叉树模型中的依赖问题。

我们还是通过一道题目来进行具体学习。

02、题目分析

示例1:

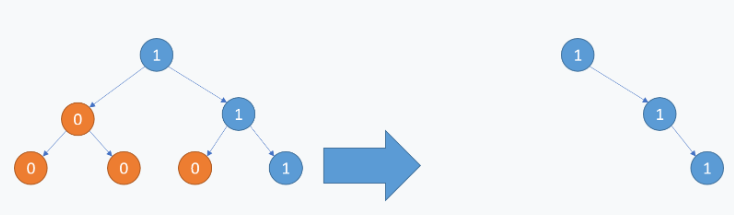
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]

解释:

• 只有红色节点满足条件“所有不包含 1 的子树”。
• 右图为返回的答案。

示例2:

输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]

示例3:

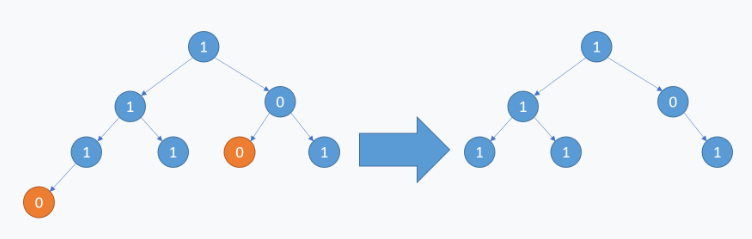
输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]

说明:

• 给定的二叉树最多有 100 个节点。
• 每个节点的值只会为 0 或 1 。

03、递归求解

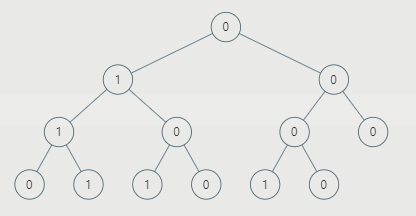
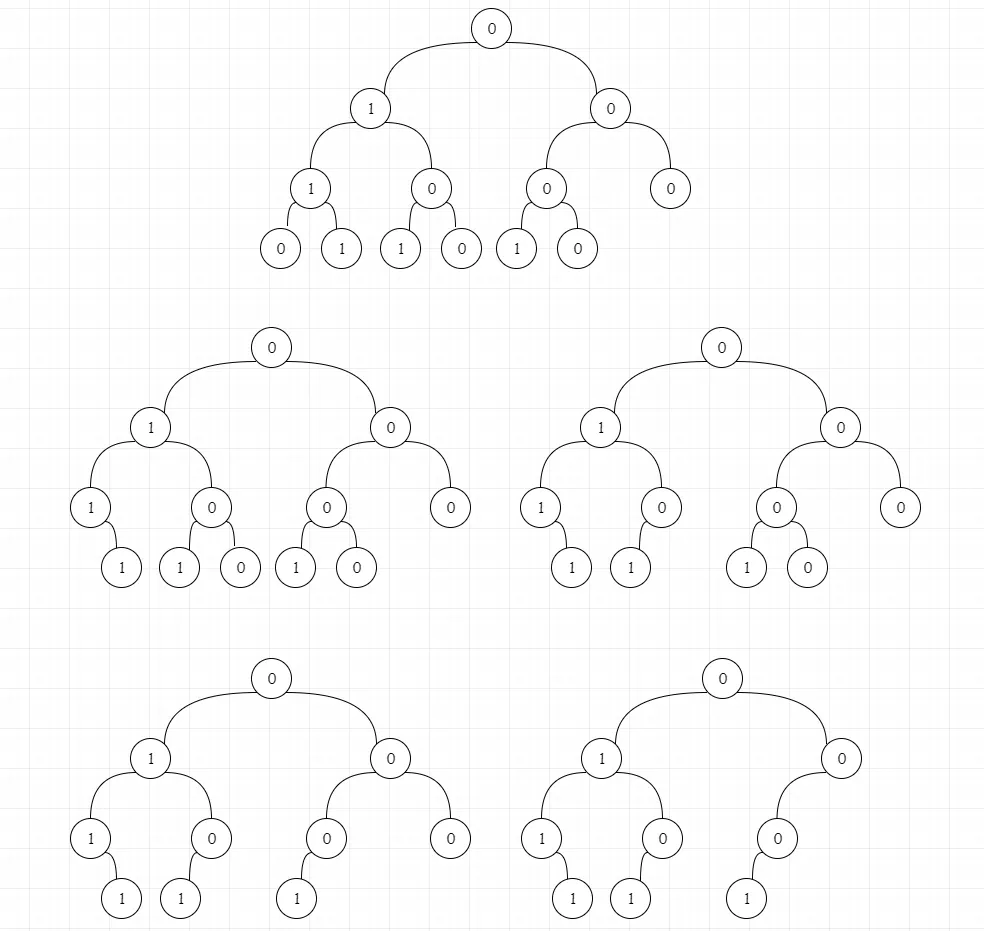
二叉树的问题，大多都可以通过递归进行求解。我们直接进行分析。假设我们有二叉树如下：[0,1,0,1,0,0,0,0,1,1,0,1,0]

就是下面这样：

剪枝之后是这样：

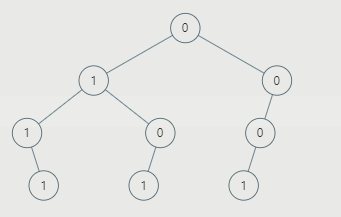
剪什么大家应该都能理解。那关键是怎么剪？过程也很简单，在递归的过程中，如果当前结点的左右节点皆为空，且当前结点为0，我们就将当前节点剪掉即可。

根据分析，很自然得出代码：

func pruneTree(root *TreeNode) *TreeNode {
    return deal(root)
}
func deal(node *TreeNode) *TreeNode {
    if node == nil {
        return nil
    }
    node.Left = deal(node.Left)
    node.Right = deal(node.Right)
    if node.Left == nil && node.Right == nil && node.Val == 0 {
        return nil
    }
    return node
}

运行结果：

我一度认为算法题的意义绝不简简单单只是为了面试，一度想把这种观念传递给认识我的朋友们。至少在工作中，对于栈，优先队列，红黑树，图等知识或多或少都是有机会能用到。不记得是不是李开复说的了，算法是提高智商少数为之可行的手段。真心希望大家可以在这个过程中为之成长，我们大家一起努力啊。