-

搜索二维矩阵（74）

问：程序员最讨厌康熙的哪个儿子。

答：胤禩。


今天依旧给大家分享一个面试的高频题目。话不多，来看题吧。


01、题目示例

这道题目非常的高频！看起来是在考察矩阵搜索，其实和矩阵一点关系都没有….


第74题：搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。


该矩阵具有如下特性：

  • 每行中的整数从左到右按升序排列。
  • 每行的第一个整数大于前一行的最后一个整数。


示例 1:

  1. 输入:
  2. matrix = [
  3.   [1,   3,  5,  7],
  4.   [10, 11, 16, 20],
  5.   [23, 30, 34, 50]
  6. ]
  7. target = 3
  9. 输出: true

示例 2:

  1. 输入:
  2. matrix = [
  3.   [1,   3,  5,  7],
  4.   [10, 11, 16, 20],
  5.   [23, 30, 34, 50]
  6. ]
  7. target = 13
  9. 输出: false


题目本身还是比较容易理解的，没有太多额外补充。


02、题解分析

说白了，这就是一道考察二分的题目。


最重要的是题中给出的两个条件：


  • 每行的第一个整数大于前一行的最后一个整数。

  • 每行中的整数从左到右按升序排列。


第一个条件意味着可以通过二分搜索确定哪行；

第二个条件意味着可以在行里进行二分搜索确定哪个元素；

PNG

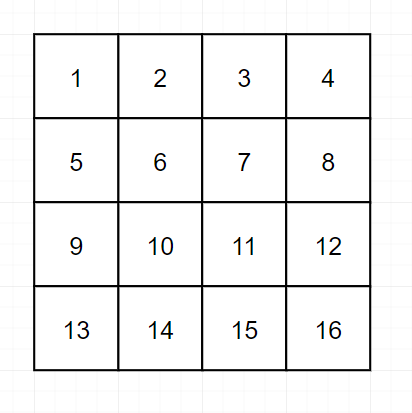
如何使用二分查找找到哪行呢？只需要一个上下边界，再每次拿着中间行最大的值和目标值比一比。

  1. //java
  2.   public int getRow(int[][] matrix, int target) {
  3.       //二分法找到target所在的行  
  4.       int top = 0, bottom = matrix.length - 1;
  5.       int col = matrix[0].length - 1;
  6.       while (top < bottom) {
  7.           int mid = (top + bottom) / 2;
  8.           if (matrix[mid][col] < target)
  9.               top = mid + 1;
  10.           else
  11.               bottom = mid;
  12.       }
  13.       return top;
  14.   }

找到是哪行之后，就和正常的二分查找没有什么区别了：

  1. //java
  2. public boolean find(int[] data, int target) {
  3.       //二分查找
  4.       int l = 0, r = data.length - 1;
  5.       while (l <= r) {
  6.           int mid = (l + r) / 2;
  7.           if (data[mid] == target)
  8.               return true;
  9.           else if (data[mid] < target)
  10.               l = mid + 1;
  11.           else
  12.               r = mid - 1;
  13.       }
  14.       return false;
  15.   }

然后再把代码拼凑到一起：

  1. //java
  2. class Solution {
  3.     public boolean searchMatrix(int[][] matrix, int target) {
  4.         if (matrix.length < 1) return false;
  5.         int row = getRow(matrix, target);
  6.         return find(matrix[row], target);
  7.     }
  9.     public int getRow(int[][] matrix, int target) {
  10.         int top = 0, bottom = matrix.length - 1;
  11.         int col = matrix[0].length - 1;
  12.         while (top < bottom) {
  13.             int mid = (top + bottom) / 2;
  14.             if (matrix[mid][col] < target)
  15.                 top = mid + 1;
  16.             else
  17.                 bottom = mid;
  18.         }
  19.         return top;
  20.     }
  22.     public boolean find(int[] data, int target) {
  23.         int l = 0, r = data.length - 1;
  24.         while (l <= r) {
  25.             int mid = (l + r) / 2;
  26.             if (data[mid] == target)
  27.                 return true;
  28.             else if (data[mid] < target)
  29.                 l = mid + 1;
  30.             else
  31.                 r = mid - 1;
  32.         }
  33.         return false;
  34.     }
  35. }

03、小知识

斐波那契数列是以兔子繁殖为例子而引入的，所以又称为“兔子数列”。指的是这样一个数列：从第3项开始，每一项都等于前两项之和。


1，1，2，3，5，8，13，21，34，55，89，144……..

PNG

(1+1=2,2+1=3,2+3=5…..21+5+8=21+13=34)

PNG


今天的题目到这里就结束了，你学会了吗？快来评论区留下你的想法吧！