只有两个键的键盘（650）

今天为大家分享一道关于 “复制” + “粘贴” 的题目。话不多说，直接看题吧。

01、题目分析

第650题：只有两个键的键盘
最初在一个记事本上只有一个字符 ‘A’ 。你每次可以对这个记事本进行两种操作：Copy All (复制全部) : 你可以复制这个记事本中的所有字符(部分的复制是不允许的)。Paste (粘贴) : 你可以粘贴你上一次复制的字符。

给定一个数字 n 。你需要使用最少的操作次数，在记事本中打印出恰好 n 个 ‘A’。输出能够打印出 n 个 ‘A’ 的最少操作次数。


示例 1:

  1. 输入: 3
  2. 输出: 3
  3. 解释:
  4. 最初, 我们只有一个字符 'A'。
  5. 第 1 步, 我们使用 Copy All 操作。
  6. 第 2 步, 我们使用 Paste 操作来获得 'AA'。
  7. 第 3 步, 我们使用 Paste 操作来获得 'AAA'。


说明:

n 的取值范围是 [1, 1000] 。

02、题目分析

本题的思路，在于想明白复制和粘贴过程中的规律，找到如何组成N个A的最小操作数。


我们从最简单的开始分析，假如我们给定数字为1，那啥也不用做，因为面板上本来就有一个A。

PNG

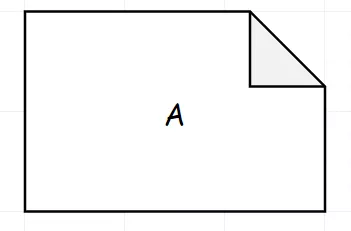
假如我们给定数字为2，那我们需要做C-P，共计2次操作来得到。

PNG

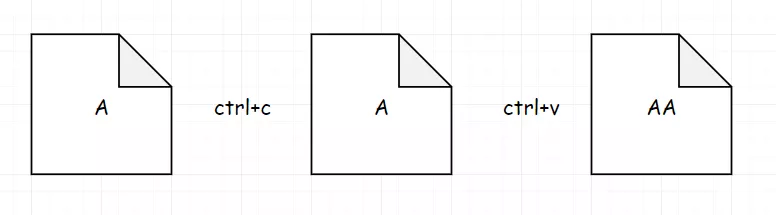
假如我们给定数字为3，那我们需要做C-P-P，共计3次操作来得到。

PNG

假如我们给定数字为4，我们发现好像变得不一样了。因为我们有两种方法都可以得到目标。（C-P-C-P）

PNG

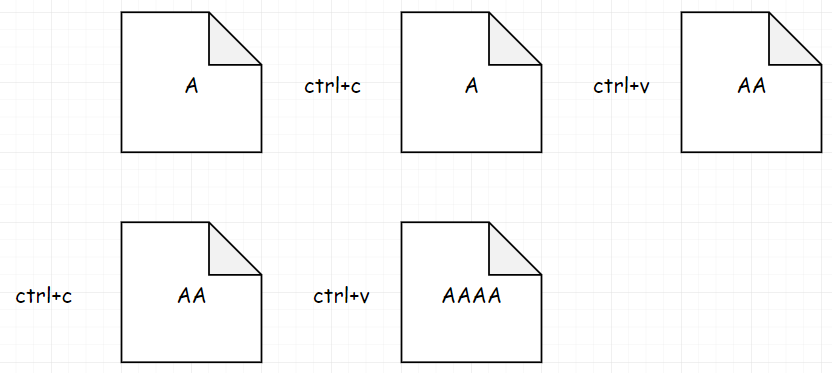
或者（C-P-P-P）

PNG

但是需要的步骤还是一样。


好了，到这里为止，STOP！通过上面的分析，我们至少可以观察出：如果 i 为质数，那么 i 是多少，就需要粘贴多少次。即：素数次数为本身的结论。如 两个A = 2，三个A = 3，五个A = 5。


那对于合数又该如何分析呢？（自然数中除能被1和本身整除外,还能被其他的数整除的数）这里我们直接给出答案：合数的次数为将其分解质因数的操作次数的和。 解释一下，这是个啥意思？举个例子：


比如30，可以分解为：325。什么意思呢？我们演示一遍：首先复制1，进行2次粘贴得到3。然后复制3，进行1次粘贴得到6。然后复制6，进行4次粘贴得到30。总共需要（CPPCPCPPPP）

PNG

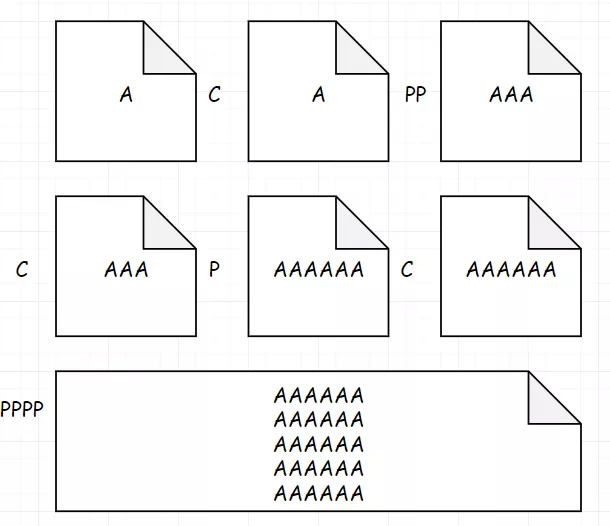
注意：这里由于每一次都需要进行一次复制，所以直接就等于分解质因数的操作次数的和。并且分解的顺序，不会影响到结果。


综合上面的分析，我们得出分析结果：

1、质数次数为其本身。

2、合数次数为将其分解到所有不能再分解的质数的操作次数的和。


03、Go语言示例

分析完毕，代码如下所示：

  1. func minSteps(n int) int {
  2.     res := 0
  3.     for i := 2; i <= n; i++ {
  4.         for n%i == 0 {
  5.             res += i
  6.             n /= i
  7.         }
  8.     }
  9.     return res
  10. }

执行结果：

PNG