不同路径

今天为大家分享一道BAT常考题目，不同路径。

01、题目示例

该题很容易出现在各大厂的面试中，一般会要求手写，所以需要完整掌握。

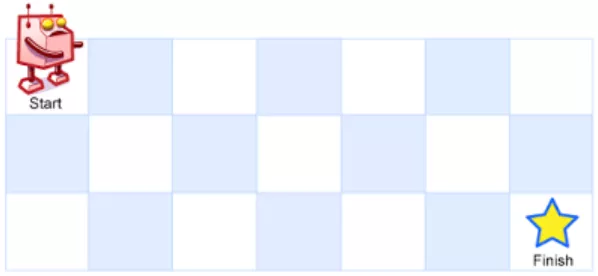
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
\1. 向右 -> 向右 -> 向下
\2. 向右 -> 向下 -> 向右
\3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

02、题目分析

这道题属于相当标准的动态规划，虽然还有一些公式法等其他解法，但是如果面试官问到，基本就是想考察你的动态规划。

拿到题目，首先定义状态。因为有横纵坐标，明显属于二维DP。我们定义DP[i][j]表示到达i行j列的最多路径。同时，因为第0行和第0列都只有一条路径，所以需要初始化为1。

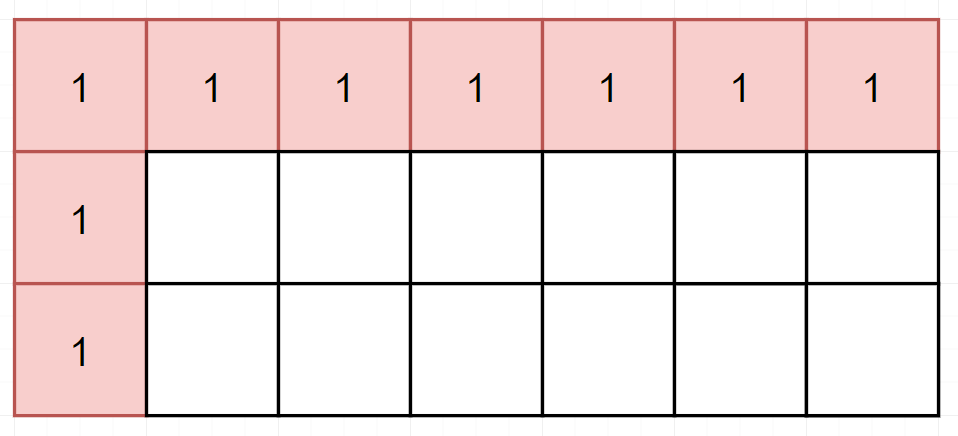
状态转移方程一目了然，dp[i][j] = dp[i-1][j] dp[i][j-1]。（想象你站在一个十字路口，到达这个十字路口可能的所有路径，就是从东南西北四个方向过来可能出现的所有路径和。放在这道题里，其实就是砍掉东南。）

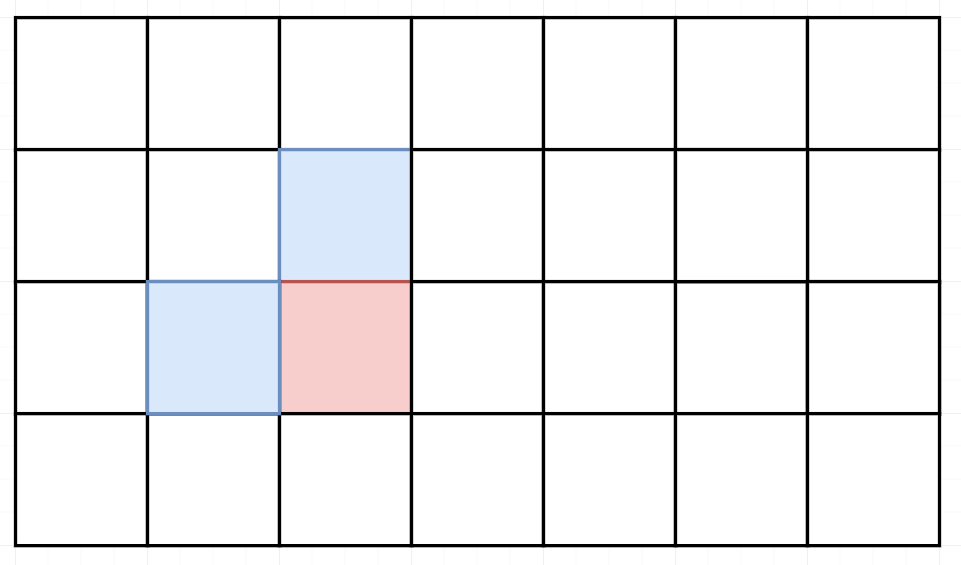
根据分析，完成代码：

//go 
func uniquePaths(m int, n int) int { 
    dp := make([][]int, m) 
    for i := 0; i < m; i   { 
        dp[i] = make([]int, n) 
    } 
    for i := 0; i < m; i   { 
        dp[i][0] = 1 
    }
    for j := 0; j < n; j   {
        dp[0][j] = 1
    }
    for i := 1; i < m; i   {
        for j := 1; j < n; j   {
            dp[i][j] = dp[i-1][j]   dp[i][j-1]
        }
    }
    return dp[m-1][n-1]
}

执行结果：

03、代码优化

上面的答案，如果在面试时给出，可以给到7分，后面3分怎么拿，我们真的需要用一个二维数组来存储吗？一起看下！

在上文中，我们使用二维数组记录状态。但是这里观察一下，每一个格子可能的路径，都是由左边的格子和上面的格子的总路径计算而来， 对于之前更早的数据，其实已经用不到了。如下图，计算第三行时，已经用不到第一行的数据了。

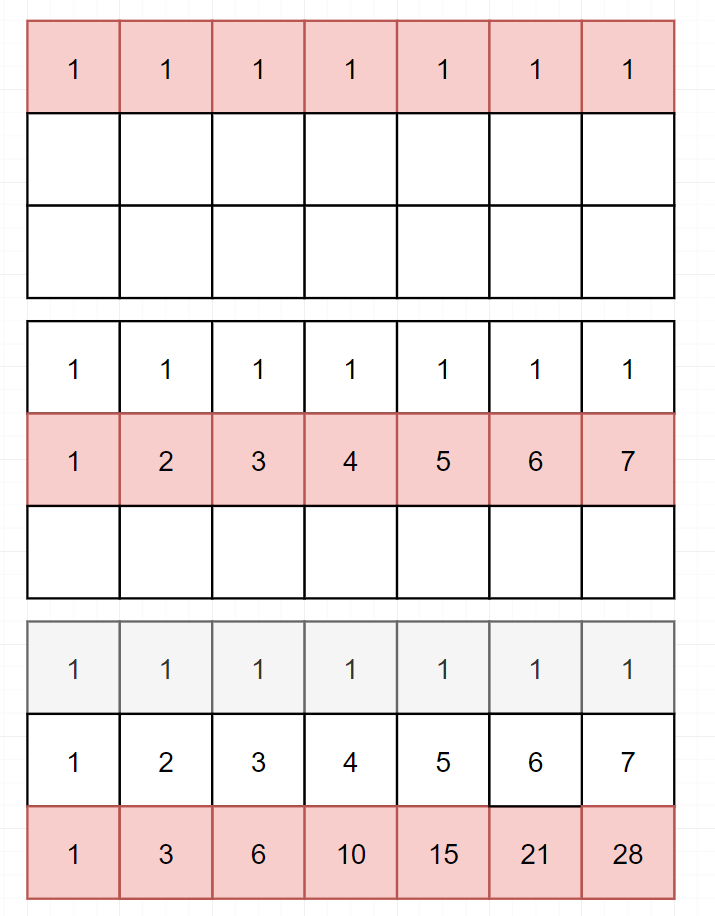
那我们只要能定义一个状态，同时可以表示左边的格子和上面的格子，是不是就可以解决问题？所以我们定义状态dp[j]，用来表示当前行到达第j列的最多路径。这个“当前行”三个字很重要，比如我们要计算dp[3]，因为还没有计算出，所以这时dp[3]保存的其实是4（上一行的数据），而dp[2]由于已经计算出了，所以保存的是6（当前行的数据）。理解了这个，就理解如何压缩状态。

最后，根据分析得出代码：

//go 
func uniquePaths(m int, n int) int { 
    dp := make([]int, n) 
    for j := 0; j < n; j   { 
        dp[j] = 1 
    } 
    for i := 1; i < m; i   { 
        for j := 1; j < n; j   { 
            //注意，这里dp[j-1]已经是新一行的数据了，而dp[j]仍然是上一行的数据
            dp[j]  = dp[j - 1]
        }
    }
    return dp[n-1]
}

执行结果：