无重复字符的最长子串（3）

在上一节中，我们使用双端队列完成了滑动窗口的一道颇为困难的题目，以此展示了什么是滑动窗口。在本节中我们将继续深入分析，探索滑动窗口题型一些具有模式性的解法。

01、滑动窗口介绍

对于大部分滑动窗口类型的题目，一般是考察字符串的匹配。比较标准的题目，会给出一个模式串B，以及一个目标串A。然后提出问题，找到A中符合对B一些限定规则的子串或者对A一些限定规则的结果，最终再将搜索出的子串完成题意中要求的组合或者其他。

比如：给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。

又或者：给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字母的最小子串。

再如：给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。

都是属于这一类的标准题型。而对于这一类题目，我们常用的解题思路，是去维护一个可变长度的滑动窗口。无论是使用双指针，还是使用双端队列，又或者用游标等其他奇技淫巧，目的都是一样的。

Now，我们通过一道题目来进行具体学习吧

02、题目分析

示例 1:

输入: "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3

示例 2:

输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。

请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。

03、题解分析

直接分析题目，假设我们的输入为“abcabcbb”，我们只需要维护一个窗口在输入字符串中进行移动。如下图：

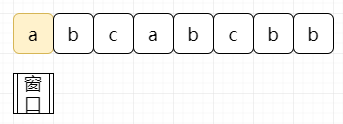
当下一个元素在窗口没有出现过时，我们扩大窗口。

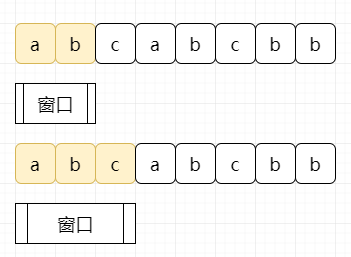
当下一个元素在窗口中出现过时，我们缩小窗口，将出现过的元素以及其左边的元素统统移出：

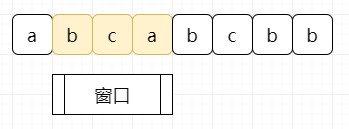
在整个过程中，我们记录下窗口出现过的最大值即可。而我们唯一要做的，只需要尽可能扩大窗口。

那我们代码中通过什么来维护这样的一个窗口呢？anyway~ 不管是队列，双指针，甚至通过map来做，都可以。

我们演示一个双指针的做法：

public class Solution {
    public static int lengthOfLongestSubstring(String s) {
        int n = s.length();
        Set<Character> set = new HashSet<>();
        int result = 0, i = 0, j = 0;
        while (i < n && j < n) {
            //charAt：返回指定位置处的字符
            if (!set.contains(s.charAt(j))) {
                set.add(s.charAt(j));
                j++;
                result = Math.max(result, j - i);
            } else {
                set.remove(s.charAt(i));
                i++;
            }
        }
        return result;
    }
}

执行结果：

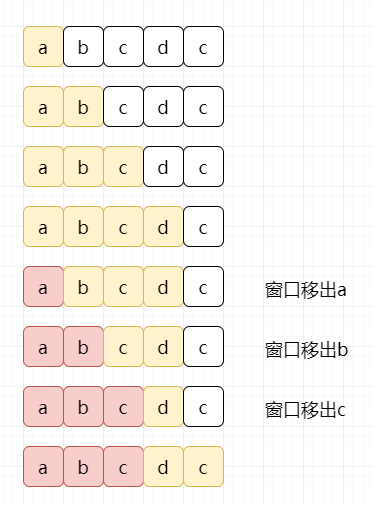
通过观察，我们能看出来。如果是最坏情况的话，我们每一个字符都可能会访问两次，left一次，right一次，时间复杂度达到了O(2N)，这是不可饶恕的。不理解的话看下图：

假设我们的字符串为“abcdc”，对于abc我们都访问了2次。

那如何来进一步优化呢？

其实我们可以定义字符到索引的映射，而不是简单通过一个集合来判断字符是否存在。这样的话，当我们找到重复的字符时，我们可以立即跳过该窗口，而不需要对之前的元素进行再次访问。

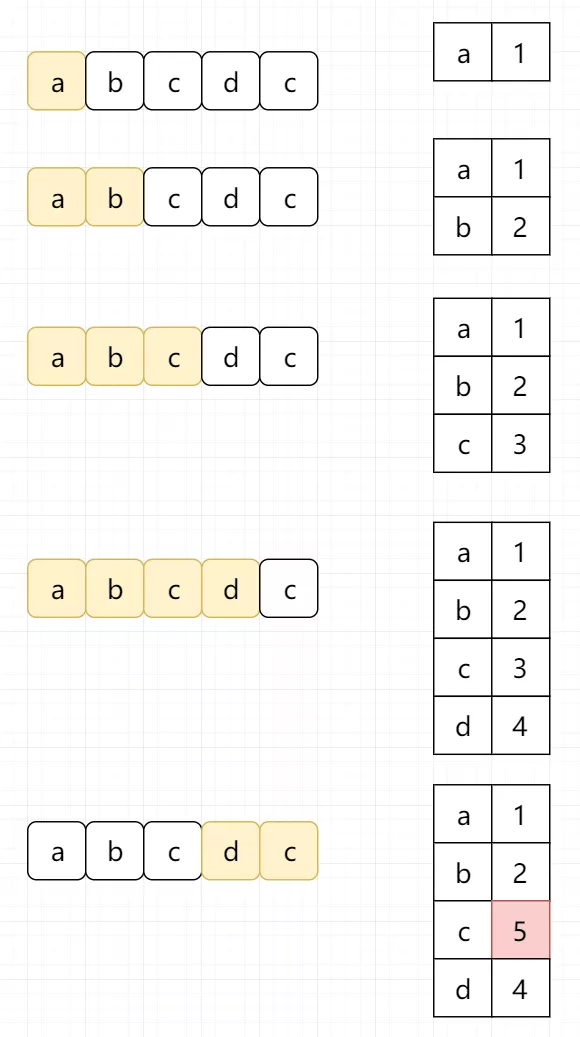
优化代码如下：

public class Solution {
    public static int lengthOfLongestSubstring(String s) {
        int n = s.length(), result = 0;
        Map<Character, Integer> map = new HashMap<>(); 
        for (int right = 0, left = 0; right < n; right++) {
            if (map.containsKey(s.charAt(right))) {
                left = Math.max(map.get(s.charAt(right)), left);
            }
            result = Math.max(result, right - left + 1);
            map.put(s.charAt(right), right + 1);
        }
        return result;
    }
}

执行结果：

修改之后，我们发现虽然时间复杂度有了一定提高，但是还是比较慢！如何更进一步的优化呢？我们可以使用一个256位的数组来替代hashmap，以进行优化。（因为ASCII码表里的字符总共有128个。ASCII码的长度是一个字节，8位，理论上可以表示256个字符，但是许多时候只谈128个。具体原因可以下去自行学习~）

进一步优化代码：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int n = s.length();
        int result = 0;
        int[] charIndex = new int[256];
        for (int left = 0, right = 0; right < n; right++) {
            char c = s.charAt(right);
            left = Math.max(charIndex[c], left);
            result = Math.max(result, right - left + 1);
            charIndex[c] = right + 1;
        }
        return result;
    }
}

执行结果：

我们发现优化后时间复杂度有了极大的改善！这里简单说一下原因，对于数组和hashmap访问时，两个谁快谁慢不是一定的，需要思考hashmap的底层实现，以及数据量大小。但是在这里，因为已知了待访问数据的下标，可以直接寻址，所以极大的缩短了查询时间。

04、总结

本题基本就到这里。最后要说的，一般建议如果要分析一道题，我们要压缩压缩再压缩，抽茧剥丝一样走到最后，尽可能的完成对题目的优化。不一定非要自己想到最优解，但绝对不要局限于单纯的完成题目，那样将毫无意义！