BST与其验证(98)

在上一节中，我们分别学习了DFS与BFS。在本节中，我们将继续学习一种特殊的二叉树结构 —— 二叉搜索树（BST）。

01、二叉搜索树

先看定义：二叉搜索树（Binary Search Tree），（又：二叉查找树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。


这里强调一下子树的概念：设T是有根树，a是T中的一个顶点，由a以及a的所有后裔（后代） 导出的子图称为有向树T的子树。具体来说，子树就是树的其中一个节点以及其下面的所有的节点所构成的树。


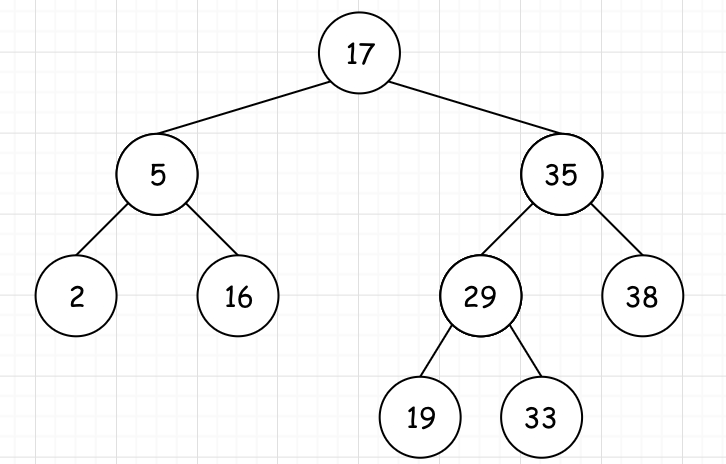
比如下面这就是一颗二叉搜索树：

img

下面这两个都不是：

img

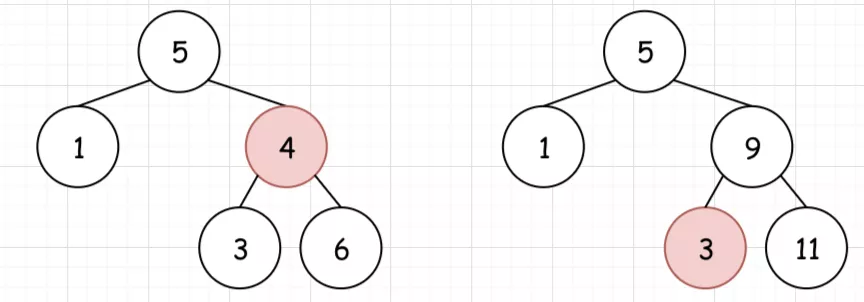
<1>图中4节点位置的数值应该大于根节点

<2>图中3节点位置的数值应该大于根节点


那我们如何来验证一颗二叉搜索树？我们看题。

02、题目分析

第98题：验证二叉搜索树
给定一个二叉树，判断其是否是一个有效的二叉搜索树。

示例 1:

  1. 输入:
  2.    5
  3.   / \
  4.  1   4
  5.     / \
  6.    3   6
  7. 输出: false
  8. 解释: 输入为: [5,1,4,null,null,3,6]。
  9.      根节点的值为 5 ，但是其右子节点值为 4 。

示例 2:

  1. 输入:
  2.     5
  3.    / \
  4.   1   4
  5.      / \
  6.     3   6
  7. 输出: false
  8. 解释: 输入为: [5,1,4,null,null,3,6]。
  9.      根节点的值为 5 ，但是其右子节点值为 4 。

首先看完题目，我们很容易想到 遍历整棵树，比较所有节点，通过 左节点值<节点值，右节点值＞节点值 的方式来进行求解。但是这种解法是错误的，因为对于任意一个节点，我们不光需要左节点值小于该节点，并且左子树上的所有节点值都需要小于该节点。（右节点一致）所以我们在此引入上界与下界，用以保存之前的节点中出现的最大值与最小值。

03、递归求解

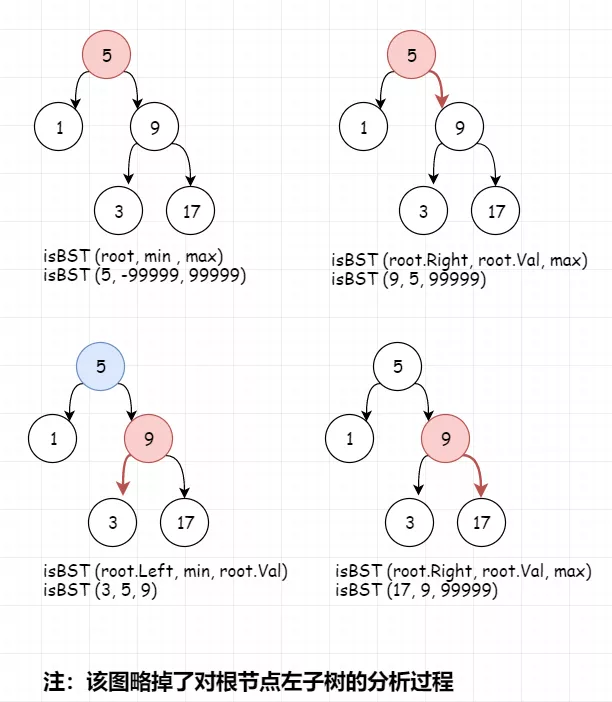
明确了题目，我们直接使用递归进行求解。这里需要强调的是，在每次递归中，我们除了进行左右节点的校验，还需要与上下界进行判断。由于该递归分析有一定难度，所以我们先展示代码：

  1. func isValidBST(root *TreeNode) bool {
  2.     if root == nil{
  3.         return true
  4.     }
  5.     return isBST(root,math.MinInt64,math.MaxInt64)
  6. }
  8. func isBST(root *TreeNode,min, max int) bool{
  9.     if root == nil{
  10.         return true
  11.     }
  12.     if min >= root.Val || max <= root.Val{
  13.         return false
  14.     }
  15.     return isBST(root.Left,min,root.Val) && isBST(root.Right,root.Val,max)
  16. }

运行结果：

img

如果觉得上文中的递归不太容易理解，可以通过下图理解：

img