最小的k个数

今天分享一道比较简单的题目，希望大家可以5分钟掌握！

01、题目示例

示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

02、堆和大小顶堆

这道题出自《剑指offer》，是一道非常高频的题目。可以通过排序等多种方法求解。但是这里，我们使用较为经典的大顶堆（大根堆）解法进行求解。因为我知道有很多人可能一脸懵逼，所以，我们先复习一下大顶堆。

首先复习一下堆，堆(Heap)是计算机科学中一类特殊的数据结构的统称，我们通常是指一个可以被看做一棵完全二叉树的数组对象。如果不记得什么是完全二叉树，可以复习这篇：

二叉树第七讲 - 完全二叉树(222)

堆的特性是父节点的值总是比其两个子节点的值大或小。如果父节点比它的两个子节点的值都要大，我们叫做大顶堆。如果父节点比它的两个子节点的值都要小，我们叫做小顶堆。

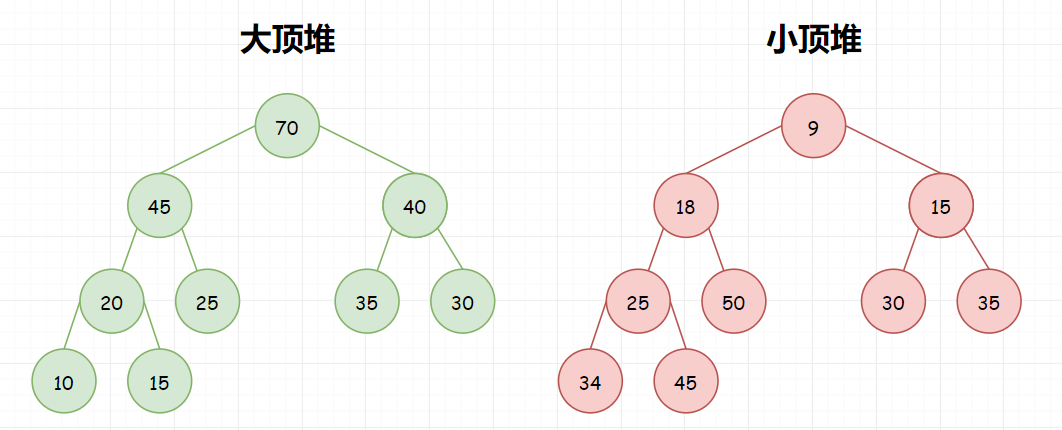
我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子。

大顶堆，满足以下公式:

arr[i] >= arr[2i 1] && arr[i] >= arr[2i 2]

小顶堆也一样：

小顶堆，满足以下公式:

arr[i] <= arr[2i 1] && arr[i] <= arr[2i 2]

03、题目分析

上面我们学习了大顶堆，现在考虑如何用大根堆进行求解。

首先，我们创建一个大小为k的大顶堆。假如数组为[4,5,1,6,2,7,3,8]，k=4。大概是下面这样：

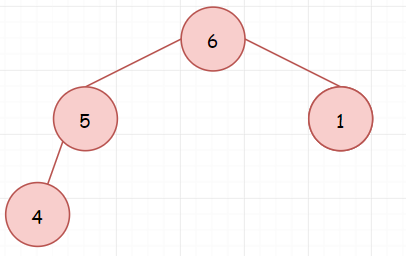
我想肯定这里有不知道如何建堆的同学。记住：对于一个没有维护过的堆（完全二叉树），我们可以从其最后一个节点的父节点开始进行调整。这个不需要死记硬背，其实就是一个层层调节的过程。

从最后一个节点的父节点调整

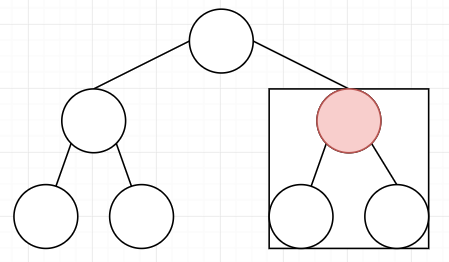
继续向上调整

继续向上调整

建堆 调整的代码大概就是这样：（翻Java牌子）

//建堆。对于一个还没维护过的堆，从他的最后一个节点的父节点开始进行调整。
private void buildHeap(int[] nums) { 
    //最后一个节点 
    int lastNode = nums.length - 1; 
    //记住：父节点 = (i - 1) / 2  左节点 = 2 * i   1  右节点 = 2 * i   2; 
    //最后一个节点的父节点 7
    int startHeapify = (lastNode - 1) / 2; 
    while (startHeapify >= 0) { 
        //不断调整建堆的过程
        heapify(nums, startHeapify--);
    }
}
    //调整大顶堆的过程
private void heapify(int[] nums, int i) {
    //和当前节点的左右节点比较，如果节点中有更大的数，那么交换，并继续对交换后的节点进行维护
    int len = nums.length;
    if (i >= len)
        return;
    //左右子节点
    int c1 = ((i << 1)   1), c2 = ((i << 1)   2);
    //假定当前节点最大
    int max = i;
    //如果左子节点比较大，更新max = c1;
    if (c1 < len && nums[c1] > nums[max]) max = c1;
    //如果右子节点比较大，更新max = c2;
    if (c2 < len && nums[c2] > nums[max]) max = c2;
    //如果最大的数不是节点i的话，那么heapify(nums, max)，即调整节点i的子树。
    if (max != i) {
        swap(nums, max, i);
        //递归处理
        heapify(nums, max);
    }
}
private void swap(int[] nums, int i, int j) {
    nums[i] = nums[i]   nums[j] - (nums[j] = nums[i]);
}

然后我们从下标 k 继续开始依次遍历数组的剩余元素。如果元素小于堆顶元素，那么取出堆顶元素，将当前元素入堆。在上面的示例中 ，因为2小于堆顶元素6，所以将2入堆。我们发现现在的完全二叉树不满足大顶堆，所以对其进行调整。

调整前

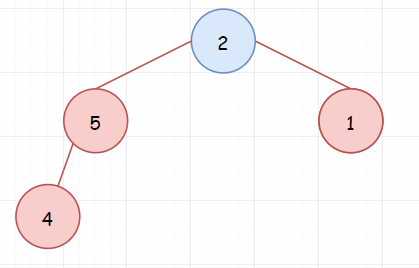
调整后

继续重复上述步骤，依次将7,3,8入堆。这里因为7和8都大于堆顶元素5，所以只有3会入堆。

调整前

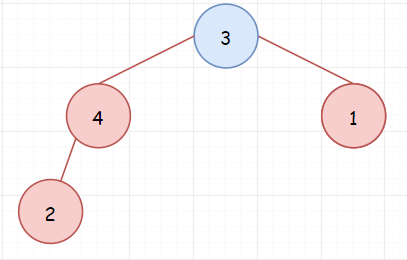
调整后

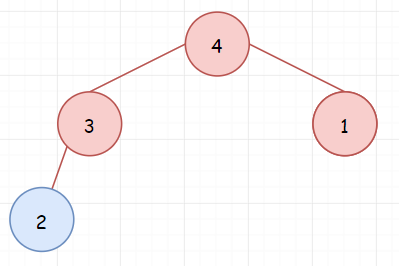
最后得到的堆，就是我们想要的结果。由于堆的大小是 K，所以这里空间复杂度是O(K)，时间复杂度是O(NlogK)。

根据分析，完成代码：

//java
class Solution { 
    public int[] getLeastNumbers(int[] arr, int k) { 
        if (k == 0) 
            return new int[0]; 
        int len = arr.length; 
        if (k == len) 
            return arr; 
        //对arr数组的前k个数建堆        
        int[] heap = new int[k];
        System.arraycopy(arr, 0, heap, 0, k);
        buildHeap(heap);
        //对后面较小的树建堆
        for (int i = k; i < len; i++) {
            if (arr[i] < heap[0]) {
                heap[0] = arr[i];
                heapify(heap, 0);
            }
        }
        //返回这个堆
        return heap;
    } 
    private void buildHeap(int[] nums) {
        int lastNode = nums.length - 1;
        int startHeapify = (lastNode - 1) / 2;
        while (startHeapify >= 0) {
            heapify(nums, startHeapify--);
        }
    }
    private void heapify(int[] nums, int i) {
        int len = nums.length;
        if (i >= len)
            return;
        int c1 = ((i << 1)   1), c2 = ((i << 1)   2);
        int max = i;
        if (c1 < len && nums[c1] > nums[max]) max = c1;
        if (c2 < len && nums[c2] > nums[max]) max = c2;
        if (max != i) {
            swap(nums, max, i);
            heapify(nums, max);
        }
    }
    private void swap(int[] nums, int i, int j) {
        nums[i] = nums[i]   nums[j] - (nums[j] = nums[i]);
    }
}

执行结果：