旋转排序数组中的最小值Ⅱ(154)
今天继续为大家讲解二分法系列篇 - 旋转排序数组最小值Ⅱ(进阶版)。话不多说,直接看题:
01、题目示例
昨天为大家讲解了元素不可重复的版本,那如果元素重复该如何处理呢?
| 第154题:旋转排序数组最小值Ⅱ |
|---|
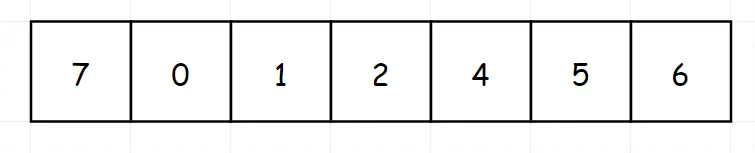
| 假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。 注意数组中可能存在重复的元素。 |
示例 1:
输入: [1,3,5]输出: 1
示例 2:
输入: [2,2,2,0,1]输出: 0
说明:
- 这道题是 旋转排序数组中的最小值(153) 的延伸题目。
- 允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
02、题目回顾
之前我也说过,通过改变题中条件,使得题目难度上升的做法。在算法题目的设计中,是一种非常常见的手段。本题就是这样,从中等变成了困难。


在讲解本题之前,首先要对昨天的题目进行一个答疑。昨天有人问我为什么题目中讲的是与left进行比较,但是最后代码中写的时候变成了和right比较。这个确实是我讲的时候讲忘了,但是这其实是一个思维转化的问题:因为在旋转之前的原数组是一个递增序列,那一定是左边的数小,右边的数大,而我们要找的是最小值,所以比较偏向左找。那如果和left进行比较,其实也是完全ok的,那我们的思路就变成了找到偏右的最大值,进而向右再移动一位,自然也就是最小值。如果不能理解的话,可以回顾一下昨天的文章:
并且我这里对昨天的题目,补上一个和left对比的版本,供大家参考学习(昨天没有给Go的示例,所以今天补一个Go的)
//gofunc findMin(nums []int) int {left, right := 0, len(nums)-1for left < right {mid := left + (right-left)>>1 + 1if nums[left] < nums[mid] {left = mid} else if nums[left] > nums[mid] {right = mid - 1}}return nums[(right+1)%len(nums)]}
上面的代码有两处需要说明,第一:mid中最后加1的目的,是为了使得mid更加靠近right,增加容错性。当然,你写到里边也是可以的,甚至更好。我怕大家看不懂,所以写在外面了。第二:最后一行代码取模,是需要考虑最大值刚好在最右边的情况。
03、题解分析
二分查找的本质,其实就是通过收敛查找空间,找到目标值的一种方式。请大家认真阅读这句话。不管是采用不同的mid定义方式,又或者是不一样的while条件,统统都是为了这个目的。在完成这个目的的基础上,我们才去考虑如何减少冗余代码,减少循环次数等等,完成进一步的优化。
现在再来看今天的题目。相对比昨天题目而言,其实只是多了nums[mid] 等于 nums[right] 时的额外处理。(当然, 如果是和left进行比较,就是nums[mid]等于nums[left])
对比一下下面两个图:
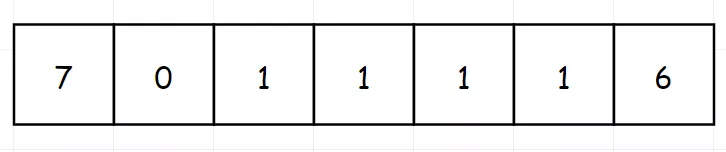
//javaclass Solution {public int findMin(int[] nums) {int left = 0;int right = nums.length - 1;while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > nums[right]) {left = mid + 1;} else if (nums[mid] < nums[right]) {right = mid;} else {right--;}}return nums[left];}};
如果我们再对比一下代码的差异,就会非常的明显:
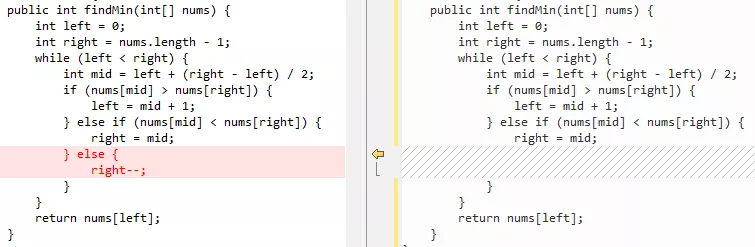
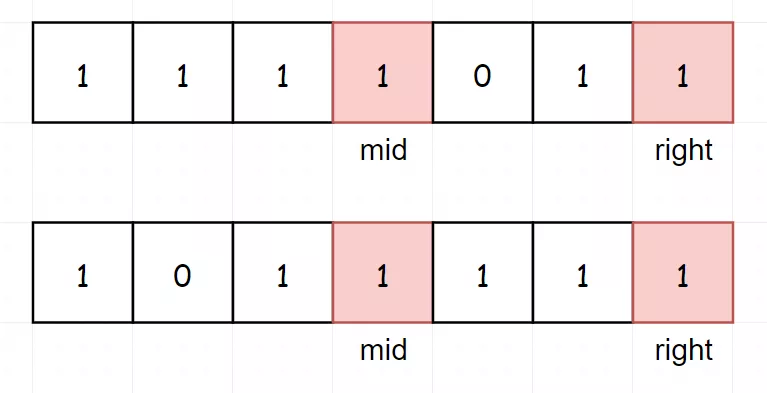
因为 mid 和 right 相等时,最小值既可能在左边,又可能在右边,所以此时自然二分思想作废,咱们就砍掉一个右边界。说白了,就是让子弹再飞一会儿。
所以,今天的问题你学会了吗,评论区留下你的想法!
