只出现一次的数字Ⅱ(137)
昨天我们在“除了某个元素只出现一次以外,其余每个元素均出现二次”的条件下,通过使用“异或”的操作,找到了只出现一次的元素。那对于其余每个元素均出现三次的case,我们应该如何解决呢?一起来看下吧。
看之前强烈建议复习昨天的文章:
01、题目示例
这种通过改变题中条件,进而增加难度的方式,其实是出题者惯用的一种手段!
| 第137题:只出现一次的数字Ⅱ |
|---|
| 给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。说明:你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗? |
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,3,2]输出: 3
示例 2:
输入: [0,1,0,1,0,1,99]输出: 99
PS:建议大家停留个两分钟先想一想…直接拉下去看题解就没什么意思了。
02、HashMap求解
很简单就能想到,说白了就是统计每个元素出现的次数,最终再返回次数为1的元素。但是使用了额外空间。
直接上代码:(go版本)
func singleNumber(nums []int) int {m := make(map[int]int)for _, k := range nums {//如果是其他语言,请注意对应的判空操作!m[k]}for k, v := range m {if v == 1 {return k}}return 0}
执行结果:

03、数学方式
这个题目曾经在Google很火~目前国内应该也有很多厂子会问到。
原理:[A,A,A,B,B,B,C,C,C] 和 [A,A,A,B,B,B,C],差了两个C。即:
3×(a b c)−(a a a b b b c)=2c
也就是说,如果把原数组去重、再乘以3得到的值,刚好就是要找的元素的2倍。举个例子:

利用这个性质,进行求解:(python代码如下,这里要注意的是,使用int可能会因为超出界限报错)
class Solution:def singleNumber(self, nums: List[int]) -> int:return int((sum(set(nums)) * 3 - sum(nums)) / 2)
执行结果:

04、位运算
对于“每个其余元素,均出现了二次”之所以可以使用“异或”进行求解,原因是因为“异或”操作可以让两数相同归 0。那对于其余元素出现三次的,是不是只要可以让其三者相同归 0,就能达到我们的目的呢?
这个思想可能比较简单,但是要让大家理解,还是有一定难度。如果大家准备好了,可以开始往下看。我看过leetcode上的题解,很多都是直接扔出来一个公式,其实讲的我认为并不是特别的清楚。所以我打算先把本题退化到“每个其余元素,均出现二次”的case来进行分析一下。
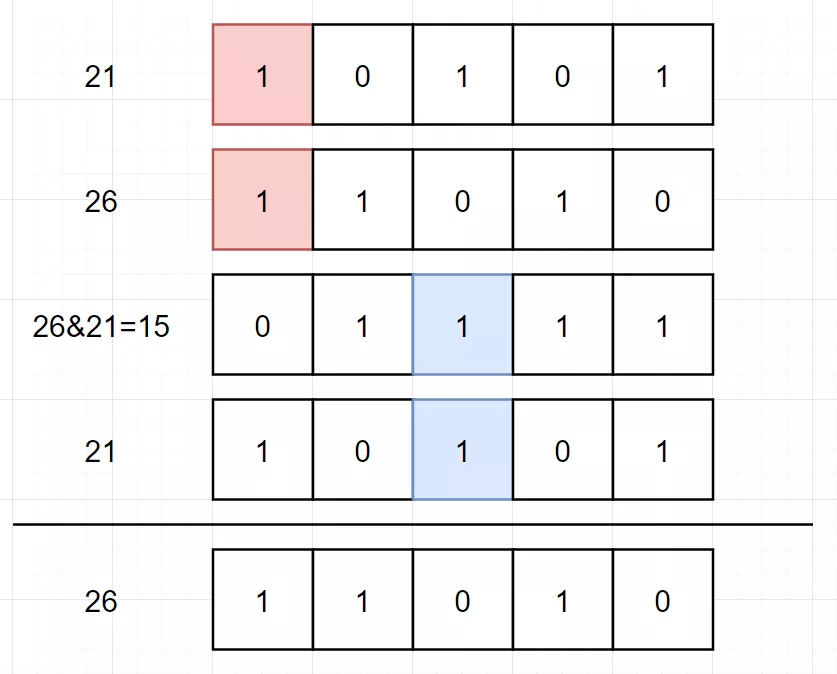
假如我们有 [21,21,26] 三个数,是下面这样:

回想一下,之所以能用“异或”,其实我们是完成了一个 同一位上有2个1清零 的过程。上面的图看起来可能容易,如果是这样 (下图应为26^21):
那对于“每个其余元素,均出现了三次”也是一样,如果我们可以完成 一个同一位上的三个1清零的过程, 也就是 a ?a ?a = 0,问题则迎刃冰解。那因为各语言中都没有这样一个现成的方法可以使用,所以我们需要构造一个。(想象一下,位运算也是造出来的对不对?)

如何构造,这里先说第一种方法(注意,到这里我们的问题已经转化成了定义一种 a ? a ? a = 0 的运算),观察一下“异或”运算:

砍掉进位的过程,是不是又可以理解为对 2 进行取模,也就是取余。到了这里,问题已经非常非常明确了。那我们要完成一个 a ? a ? a = 0 的运算,是不是其实就是让其二进制的每一位数都相加,最后再对 3 进行一个取模的过程呢?(一样,如果要定义一个 a ? a ? a ? a = 0 的运算,那就最后对 4 进行取模就可以了)
//gofunc singleNumber(nums []int) int {number, res := 0, 0for i := 0; i < 64; i++ {//初始化每一位1的个数为0number = 0for _, k := range nums {//通过右移i位的方式,计算每一位1的个数number + = (k >> i) & 1}//最终将抵消后剩余的1放到对应的位数上res |= (number) % 3 << i}return res}
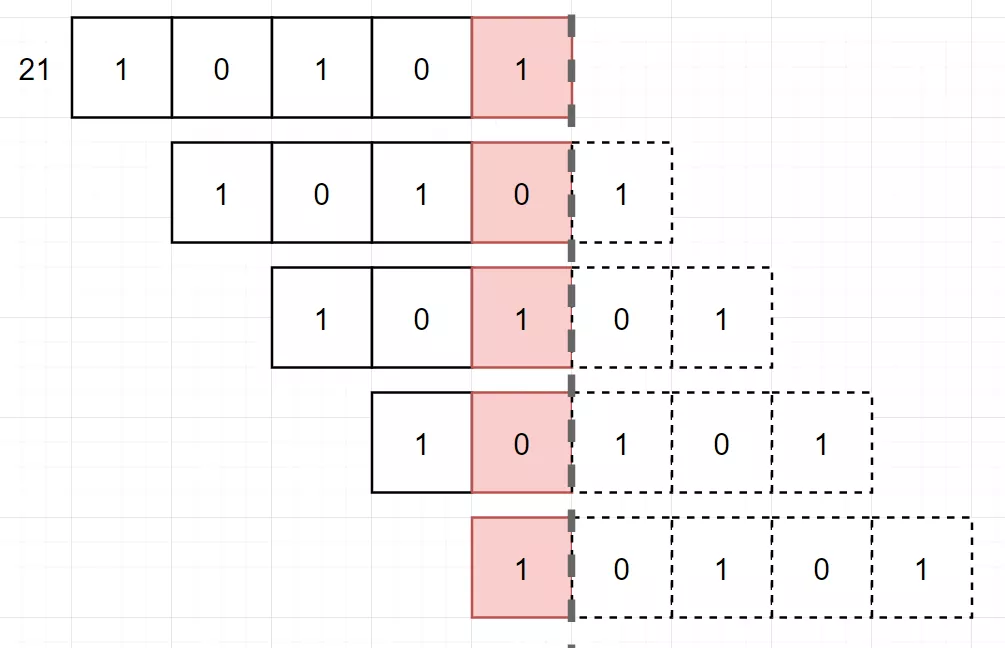
如果对上面的代码不能理解,可以看看这个图,假设只有一个数 [21],我们通过不断右移的方式,获取其每一位上的1。当然,这里因为余数都是1,所以肯定都保留了下来,然后与 1 进行 “与”运算,最终再将其放入到对应的位数上。
执行结果:

在上面的代码中,我们通过一个number,来记录每一位数出现的次数。但是缺点是,我们记录了64位(Go语言中,int为32位以上)

那如果我们可以同时对所有位进行计数,是不是就可以简化过程。因为我们的目的是把每一位与3取模进行运算,是不是就可以理解为其实是一个三进制。如果大家听不懂三进制的话,可以简单理解为3次一循环,也就是 00 - 01 - 10 - 11。但是又因为对于 11 这种情况,我们需要砍掉(上面已经说过了,相当于 11 - 00 的转化),所以我们就只有3个状态,00 - 01 - 10,所以我们采用 a 和 b 来记录状态。其中的状态转移过程如下:

这里 a‘ 和 b’ 的意思代表着 a 和 b 下一次的状态。next 代表着下一个 bit 位对应的值。然后这是什么,不就是状态机嘛。。。我们通过 a 和 b 的状态变化,来完成次数统计。
然后因为此图复杂,将其分别简化成 a 和 b 的卡诺图(卡诺图是逻辑函数的一种图形表示。两逻辑相邻项,合并为一项,保留相同变量,消去不同变量。先 b’ 后 a‘ )
| next\a,b | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 1 | 1 | 0 | X | 0 |
| 0 | 0 | 1 | X | 0 |
| next\a,b | 00 | 01 | 11 | 10 |
|---|---|---|---|---|
| 1 | 0 | 1 | X | 0 |
| 0 | 0 | 0 | X | 1 |
然后我们根据卡诺图(这个卡诺图其实并不难看。。如果学习一下话,还是挺简单的。)写出关系式:
class Solution {public int singleNumber(int[] nums) {int a = 0, b = 0, tmp = 0;for (int next : nums) {tmp = (a & ~next) | (b & next);b = (~a & ~b & next) | (b & ~next);a = tmp;}return b;}}
当然,其实题解还可以再进一步优化,其实就是化简上一步中的公式:
class Solution {public int singleNumber(int[] nums) {int a = 0, b = 0;for (int next : nums) {b = (b ^ next) & ~a;a = (a ^ next) & ~b; 7 }return b;}}
当然,这个解法就相当牛皮了,反正我第一次做肯定是想不到的。。。我看了一下,第一个给出这个解法的人,应该是一位国外的工程师(某扣上面有很多人其实都是把题解翻译过来的,当然我有时也会哈哈哈哈,我觉得这某种意义上讲也是一个好的现象,挺好)不过毕竟非原创,还是得说明一下!
总之,今天的题目,有一定的难度!希望大家动脑动手动脚, 认真想想。
所以,今天的问题你学会了吗?评论区留下你的想法!
