只出现一次的数字(136)

今天仍然分享一道关于位运算颇为简单的题型，同时，从明天开始将会提高难度，大家做好准备。

01、题目示例

这道题，大家先想一想是用什么思路进行求解？


第136题：只出现一次的数字
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？


示例 1:

  1. 输入: [2,2,1]
  2. 输出: 1

示例 2:

  1. 输入: [4,1,2,1,2]
  2. 输出: 4


PS：建议大家停留个两分钟先想一想…直接拉下去看题解就没什么意思了。

02、题目分析

位运算的题目我们已经讲了好几道了，这道也不例外，也是其中一个非常典型的例子！属于必须掌握的题型。


直接分析，我们要找只出现一次的数字，并且已知了其他的数字都只出现了两次。那么这种一听其实就应该想到需使用位运算来进行求解。最好的，就是在读完题目的瞬间，直接条件反射！（当然，如果你现在第一反应是想到 通过遍历统计，或者其他如使用hashmap 等方式来进行求解，那我觉得你的位运算这块，是有必要加强练习力度的。如果你第一反应，连思路都没有，那我觉得对于整个算法的能力这块，都是比较欠缺的，需要下苦功！）


回到题目，如何使用位运算进行求解呢？对于任意两个数a和b，我们对其使用 “异或”操作，应该有以下性质：

  • 任意一个数和0异或仍然为自己：
a⊕0 = a

  • 任意一个数和自己异或是0：

    a⊕a=0

  • 异或操作满足交换律和结合律：

    a⊕b⊕a=(a⊕a)⊕b=0⊕b=b

可能有人直接都不知道异或是什么，所以还是举个例子，比如5异或3，也就是5⊕3，也就是5^3，是下面这样：

PNG

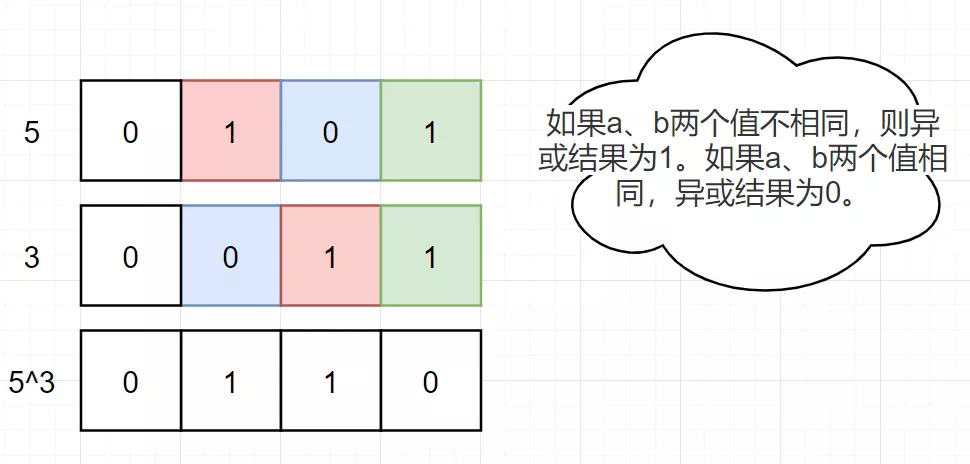
根据分析，得出代码：（c 版本）

  1. //CPP
  2. class Solution {
  3. public:
  4.     int singleNumber(vector<int>& nums) {
  5.         int ans = 0;
  6.         for (int num : nums) {
  7.             ans ^= num;
  8.         }
  9.         return ans;
  10.     }
  11. };

（java版本）

  1. //JAVA
  2. class Solution {
  3.     public int singleNumber(int[] nums) {
  4.         int ans = nums[0];
  5.             for (int i = 1; i < nums.length; i++) {
  6.                 ans = ans ^ nums[i];
  7.             }
  8.         return ans;
  9.     }
  10. }

(python版本)

  1. //py
  2. class Solution:
  3.     def singleNumber(self, nums: List[int]) -> int:
  4.         res = 0
  5.         for i in range(len(nums)):
  6.             res ^= nums[i]
  7.         return res

执行结果：

PNG

03、题目进阶

如果修改上面的题目，除了某个元素只出现一次，其余元素都出现了3次以上，那么该如何求解？


修改一个条件之后，本题的难度大幅度提升！“异或”的方式看起来似乎没办法运用在“其余数出现3次以上”的条件中。那对于这种问题又该如何求解？我这里给出几种思路，大家下去分析一下，明天我会公布这道衍化题型的解决方案：


  • 思路1：使用hashmap，统计每个数字出现的次数，最后返回次数为1的数字。。。然后等待一段时间，接到很遗憾的通知。

  • 思路2：上面的题目，对于相同的两个数，进行异或运算，我们可以进行“抵消”，那是否可以找到一种方式，来让相同的三个数进行相互抵消呢？

  • 思路3：是不是可以通过数学的方式来进行计算？


所以，今天的问题你学会了吗？评论区留下你的想法！