BST 的删除(450)

在两节中，我们了解了BST（二叉搜索树）的概念，并且知道了如何在BST中查找一个元素。那我们又如何在BST中去删除一个元素呢？我们将通过本节的例题进行学习！

下面我们仍然通过例题进行讲解。

01、题目分析

一般来说，删除节点可分为两个步骤：

• 首先找到需要删除的节点；
• 如果找到了，删除它。

说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

示例：

root = [5,3,6,2,4,null,7]
key = 3
    5
   / \
  3   6
 / \   \
2   4   7
给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
    5
   / \
  4   6
 /     \
2       7
另一个正确答案是 [5,2,6,null,4,null,7]。
    5
   / \
  2   6
   \   \
    4   7

强烈建议先学习之前两节内容！

以达到最好的学习效果！

02、复习巩固

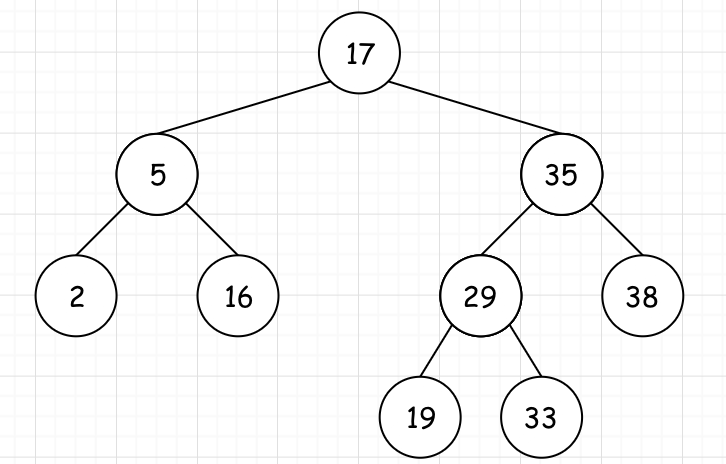
先复习一下，二叉搜索树（BST）的特性：

• 若它的左子树不为空，则所有左子树上的值均小于其根节点的值
• 若它的右子树不为空，则所有右子树上的值均大于其根节点得值
• 它的左右子树也分别为二叉搜索树

如下图就是一棵典型的BST：

03、图解分析

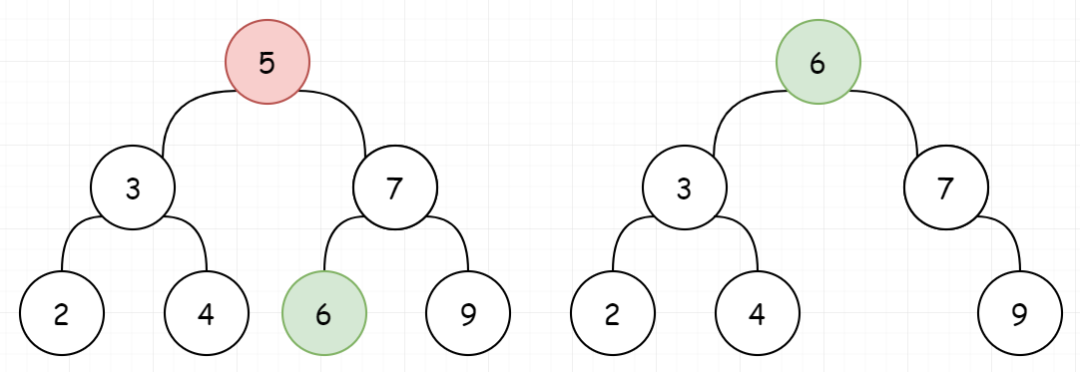
明确了概念，我们进行分析。我们要删除BST的一个节点，首先需要找到该节点。而找到之后，会出现三种情况。

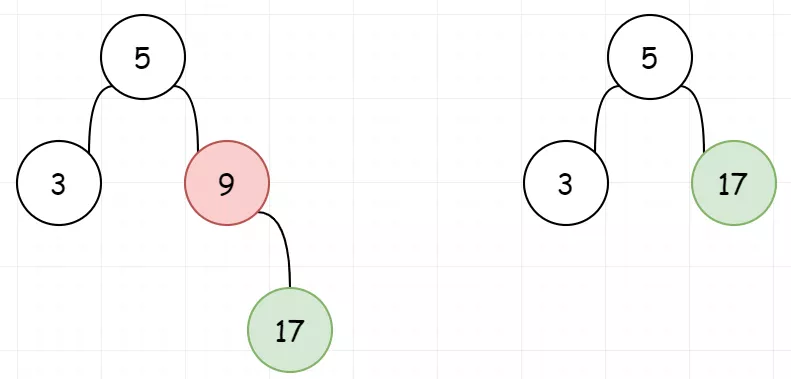
1、待删除的节点左子树为空，让待删除节点的右子树替代自己。

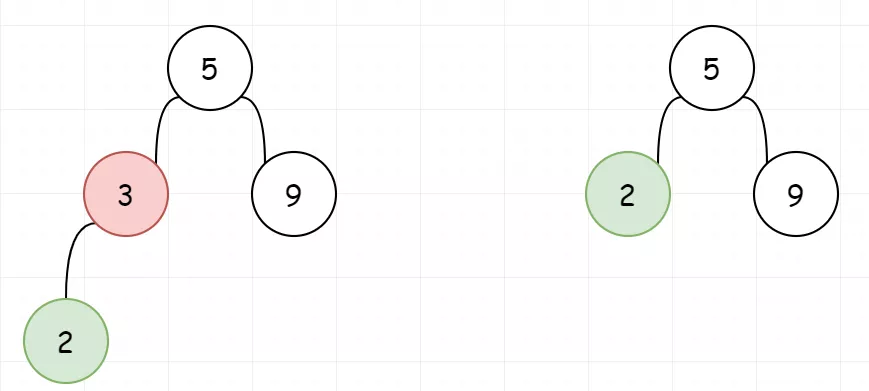
2、待删除的节点右子树为空，让待删除节点的左子树替代自己。

3、如果待删除的节点的左右子树都不为空。我们需要找到比当前节点小的最大节点（前驱），来替换自己

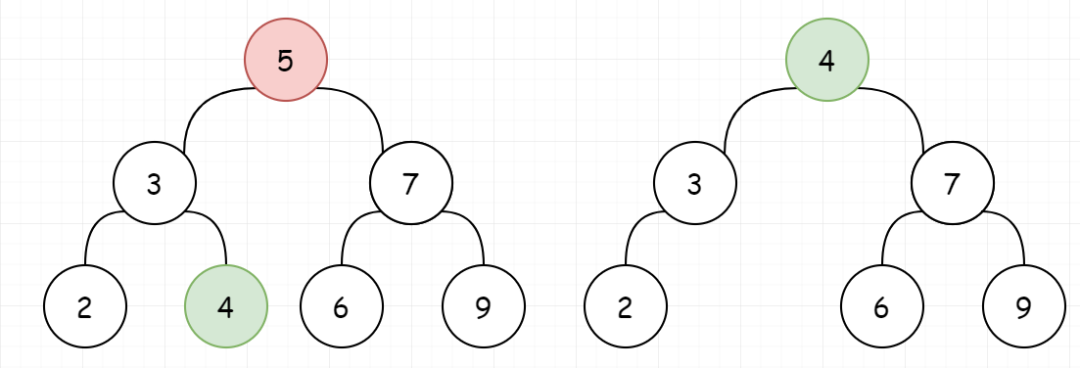
或者比当前节点大的最小节点（后继），来替换自己。

分析完毕，我们一起看代码怎么实现吧。

04、GO语言示例

这里我们给出通过后继节点来替代自己的方案（请后面自行动手实现另一种方案）：

func deleteNode(root *TreeNode, key int) *TreeNode {
    if root == nil {
        return nil
    }
    if key < root.Val {
        root.Left = deleteNode( root.Left, key )
        return root
    }
    if key > root.Val {
        root.Right = deleteNode( root.Right, key )
        return root
    }
    //到这里意味已经查找到目标
    if root.Right == nil {
        //右子树为空
        return root.Left
    }
    if root.Left == nil {
        //左子树为空
        return root.Right
    }
    minNode := root.Right
    for minNode.Left != nil {
        //查找后继
        minNode = minNode.Left
    }
    root.Val = minNode.Val
    root.Right = deleteMinNode( root.Right )
    return root
}
func deleteMinNode( root *TreeNode ) *TreeNode {
    if root.Left == nil {
        pRight := root.Right
        root.Right = nil
        return pRight
    }
    root.Left = deleteMinNode( root.Left )
    return root
}

执行结果：