BST 的查找(700)

在上一节中，我们学习了二叉搜索树。那我们如何在二叉搜索树中查找一个元素呢？和普通的二叉树又有何不同？我们将在本节内容中进行学习！

下面我们仍然通过例题进行讲解。

01、题目分析

第700题：二叉搜索树中的搜索
给定二叉搜索树（BST）的根节点和一个值。你需要在 BST 中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL 。

示例：

  1. 给定二叉搜索树:
  3.         4
  4.        / \
  5.       2   7
  6.      / \
  7.     1   3
  9. 和值: 2

你应该返回如下子树:

  1.       2     
  2.      / \   
  3.     1   3

在上述示例中，如果要找的值是 5 ，但因为没有节点值为 5 ，我们应该返回 NULL 。


本题为必须掌握! 需要非常熟悉

为后续题目打基础！

02、复习巩固

先复习一下，二叉搜索树（BST）的特性：


  • 若它的左子树不为空，则所有左子树上的值均小于其根节点的值
  • 若它的右子树不为空，则所有右子树上的值均大于其根节点得值
  • 它的左右子树也分别为二叉搜索树


如下图就是一棵典型的BST：

img

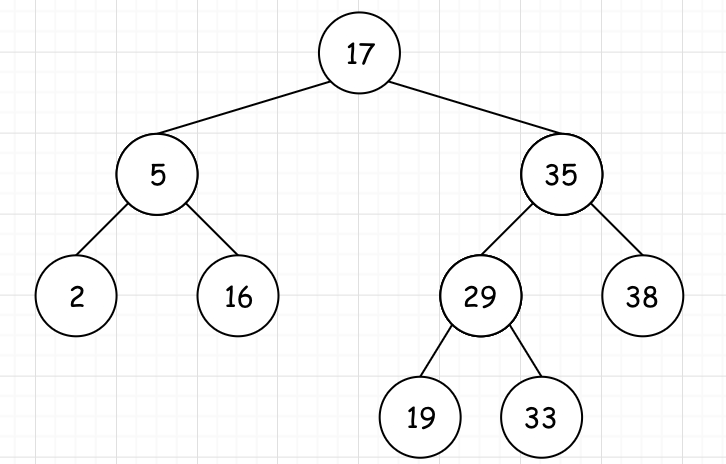
03、图解分析

假设目标值为 val，根据BST的特性，我们可以很容易想到查找过程


  • 如果val小于当前结点的值，转向其左子树继续搜索；
  • 如果val大于当前结点的值，转向其右子树继续搜索；
  • 如果已找到，则返回当前结点。

img

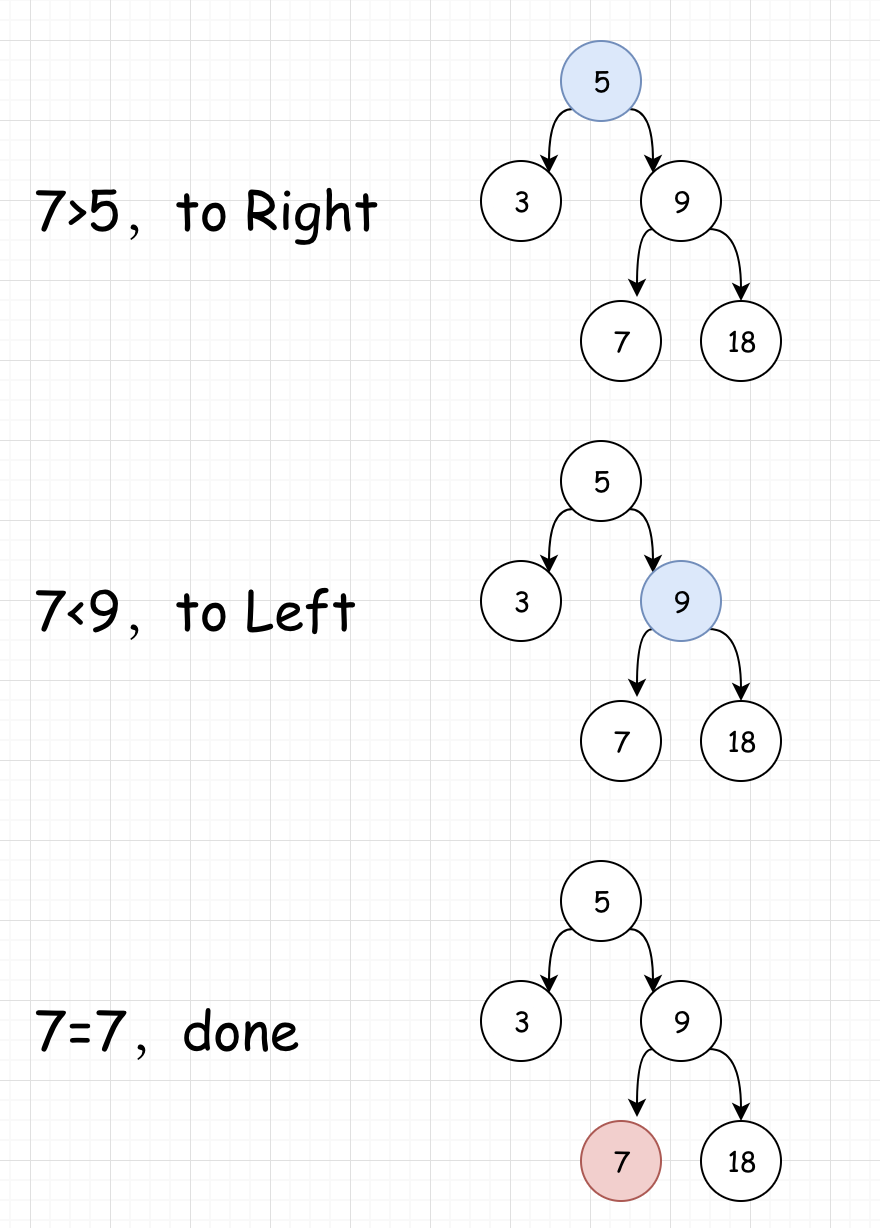
很简单，不是吗？

04、代码示例

给出递归和迭代两种解法：

  1. //递归 
  2. public TreeNode searchBST(TreeNode root, int val) { 
  3.     if (root == null) 
  4.         return null; 
  5.     if (root.val > val) { 
  6.         return searchBST(root.left, val);    
  7.     } else if (root.val < val) {
  8.         return searchBST(root.right, val);
  9.     } else {
  10.         return root;
  11.     }
  12. }
  13. //迭代
  14. public TreeNode searchBST(TreeNode root, int val) {
  15.         while (root != null) {
  16.             if (root.val == val) {
  17.                 return root;
  18.             } else if (root.val > val) {
  19.                 root = root.left;
  20.             } else {
  21.                 root = root.right;
  22.             }
  23.         }
  24.         return null;
  25.  }


递归与迭代的区别


递归：重复调用函数自身实现循环称为递归；

迭代：利用变量的原值推出新值称为迭代，或者说迭代是函数内某段代码实现循环；

特别说明


本题确实很简单！专门拉出来讲解的目的有二。第一BST确实很重要，第二希望通过重复，能加深大家对BST的印象，不至于和后面的内容出现交叉感染！