层次遍历与BFS(102)

在上一节中，我们通过例题学习了二叉树的DFS（深度优先搜索），其实就是沿着一个方向一直向下遍历。那我们可不可以按照高度一层一层的访问树中的数据呢？当然可以，就是本节中我们要讲的BFS（宽度优先搜索），同时也被称为广度优先搜索。

我们仍然通过例题进行讲解。

01、题目分析

示例:

给定二叉树 [3,9,20,null,null,15,7]，
    3   
   / \  
  9  20    
    /  \  
   15   7
返回其层次遍历结果：[[3],[9,20],[15,7]]

本系列内容均为必须掌握！

02、BFS介绍

BFS，广度/宽度优先。其实就是从上到下，先把每一层遍历完之后再遍历一下一层。假如我们的树如下：

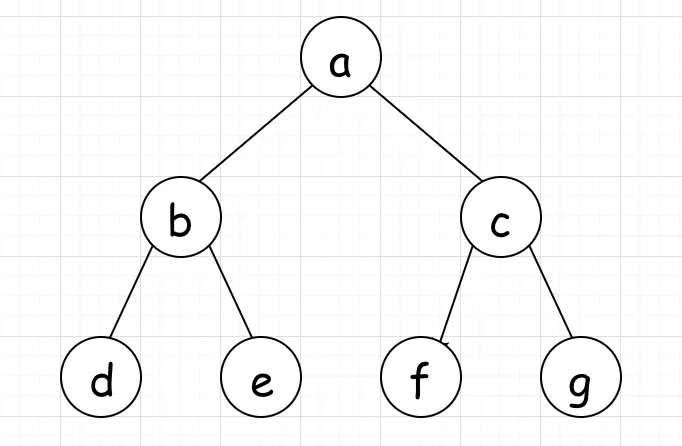
按照BFS，访问顺序如下：

a->b->c->d->e->f->g

了解了BFS，我们开始对本题进行分析。

03、递归求解

同样，我们先考虑本题的递归解法。想到递归，我们一般先想到DFS。我们可以对该二叉树进行先序遍历（根左右的顺序），同时，记录节点所在的层次level，并且对每一层都定义一个数组，然后将访问到的节点值放入对应层的数组中。

假设给定二叉树为[3,9,20,null,null,15,7]，图解如下：

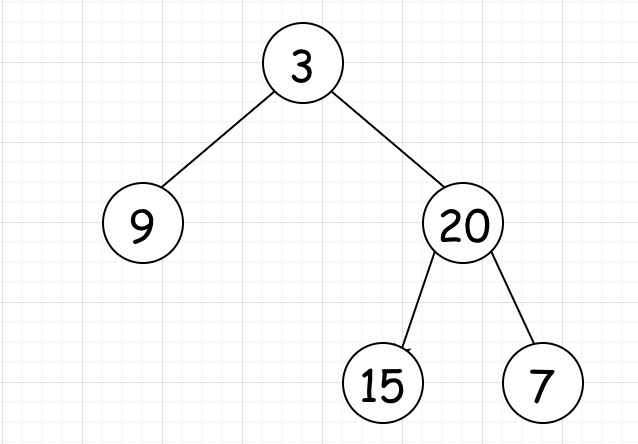
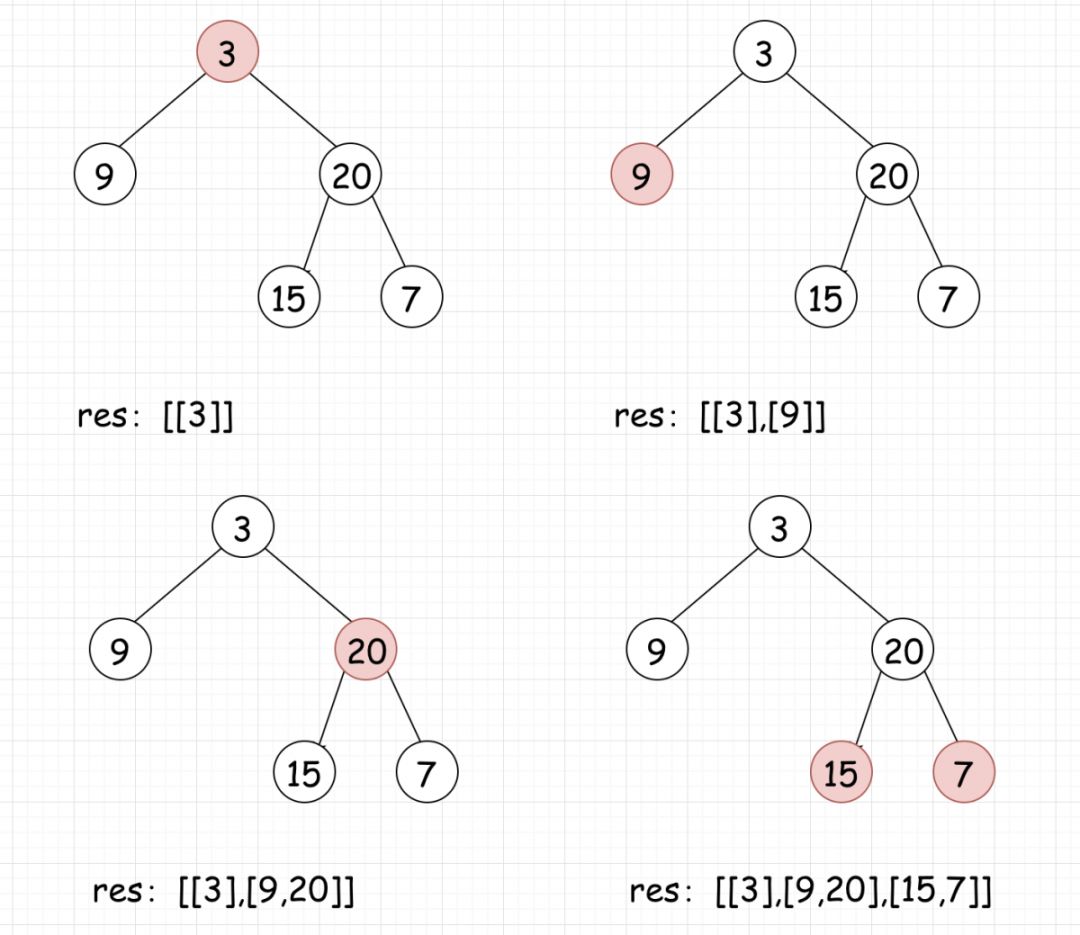
根据以上分析，代码如下：

func levelOrder(root *TreeNode) [][]int {
    return dfs(root, 0, [][]int{})
}
func dfs(root *TreeNode, level int, res [][]int) [][]int {
    if root == nil {
        return res
    }
    if len(res) == level {
        res = append(res, []int{root.Val})
    } else {
        res[level] = append(res[level], root.Val)
    }
    res = dfs(root.Left, level+1, res)
    res = dfs(root.Right, level+1, res)
    return res
}

04、BFS求解

上面的解法，其实相当于是用DFS的方法实现了二叉树的BFS。那我们能不能直接使用BFS的方式进行解题呢？当然，我们可以使用Queue的数据结构。我们将root节点初始化进队列，通过消耗尾部，插入头部的方式来完成BFS。

具体步骤如下图：

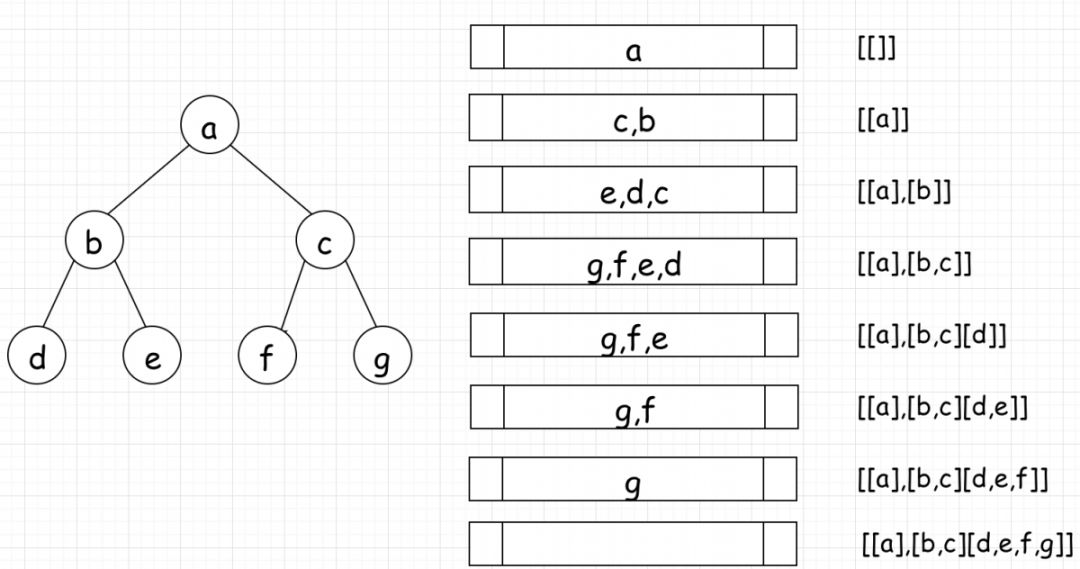
根据以上分析，代码如下：

func levelOrder(root *TreeNode) [][]int {
    var result [][]int
    if root == nil {
        return result
    }
    // 定义一个双向队列
    queue := list.New()
    // 头部插入根节点
    queue.PushFront(root)
    // 进行广度搜索
    for queue.Len() > 0 {
        var current []int
        listLength := queue.Len()
        for i := 0; i < listLength; i++ {
            // 消耗尾部
            // queue.Remove(queue.Back()).(*TreeNode)：移除最后一个元素并将其转化为TreeNode类型
            node := queue.Remove(queue.Back()).(*TreeNode)
            current = append(current, node.Val)
            if node.Left != nil {
                //插入头部
                queue.PushFront(node.Left)
            }
            if node.Right != nil {
                queue.PushFront(node.Right)
            }
        }
        result = append(result, current)
    }
    return result
}