最大深度与DFS(104)
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。树比链表稍微复杂,因为链表是线性数据结构,而树不是。树的问题很多都可以由广度优先搜索或深度优先搜索解决。
在本系列中,我们将通过一些例题,学习关于二叉树的经典操作!
01、题目分析
| 第104题:二叉树的最大深度 |
|---|
| 给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数 |
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],3/ \9 20/ \15 7
02、递归求解
我们知道,每个节点的深度与它左右子树的深度有关,且等于其左右子树最大深度值加上 1 。 即:
maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1
以 [3,4,20,null,null,15,7] 为例:
<1>我们要对根节点的最大深度求解,就要对其左右子树的深度进行求解
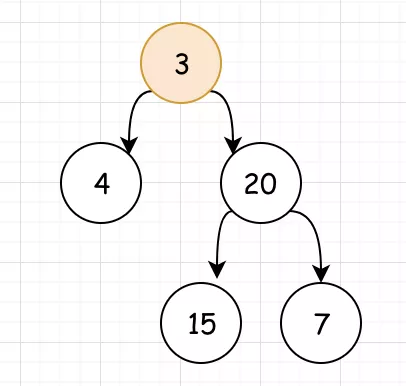
<2>我们看出。以4为根节点的子树没有左右节点,其深度为 1 。而以 20 为根节点的子树的深度,同样取决于它的左右子树深度。
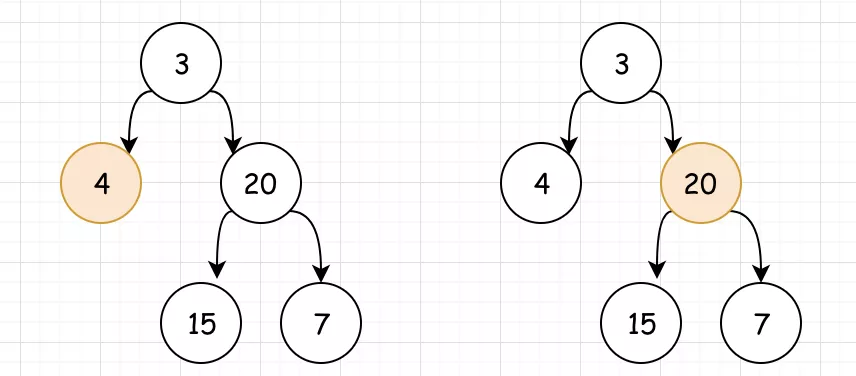
<3>对于15和7的子树,我们可以一眼看出其深度为 1 。
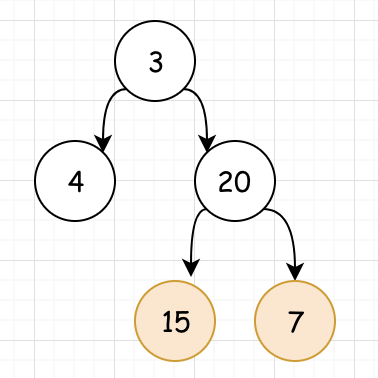
<4>由此我们可以得到根节点的最大深度为:
maxDepth(root-3)=max(**maxDepth**(sub-4),**maxDepth**(sub-20))+1=max(1,max(**maxDepth**(sub-15),**maxDepth**(sub-7))+1)+1=max(1,max(1,1)+1)+1=max(1,2)+1=3
根据分析,我们通过递归进行求解代码如下:
func maxDepth(root *TreeNode) int {if root == nil {return 0}return max(maxDepth(root.Left), maxDepth(root.Right)) + 1}func max(a int, b int) int {if a > b {return a}return b}
03、DFS
其实我们上面用的递归方式,本质上是使用了DFS的思想。先介绍一下DFS:深度优先搜索算法(Depth First Search),对于二叉树而言,它沿着树的深度遍历树的节点,尽可能深的搜索树的分支,这一过程一直进行到已发现从源节点可达的所有节点为止。

如上图二叉树,它的访问顺序为:
A-B-D-E-C-F-G
A-B-D-E-C-F-G
到这里,我们思考一个问题?虽然我们用递归的方式根据DFS的思想顺利完成了题目。但是这种方式的缺点却显而易见。因为在递归中,如果层级过深,我们很可能保存过多的临时变量,导致栈溢出。这也是为什么我们一般不在后台代码中使用递归的原因。如果不理解,下面我们详细说明:
事实上,函数调用的参数是通过栈空间来传递的,在调用过程中会占用线程的栈资源。而递归调用,只有走到最后的结束点后函数才能依次退出,而未到达最后的结束点之前,占用的栈空间一直没有释放,如果递归调用次数过多,就可能导致占用的栈资源超过线程的最大值,从而导致栈溢出,导致程序的异常退出。
所以,我们引出下面的话题:如何将递归的代码转化成非递归的形式。这里请记住,99%的递归转非递归,都可以通过栈来进行实现。
非递归的DFS,代码如下:
private List<TreeNode> traversal(TreeNode root) { List<TreeNode> res = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();stack.add(root);while (!stack.empty()) {TreeNode node = stack.peek();res.add(node);stack.pop();if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return res;}
上面的代码,唯一需要强调的是,为什么需要先右后左压入数据?是因为我们需要将先访问的数据,后压入栈(请思考栈的特点)。
如果不理解代码,请看下图:
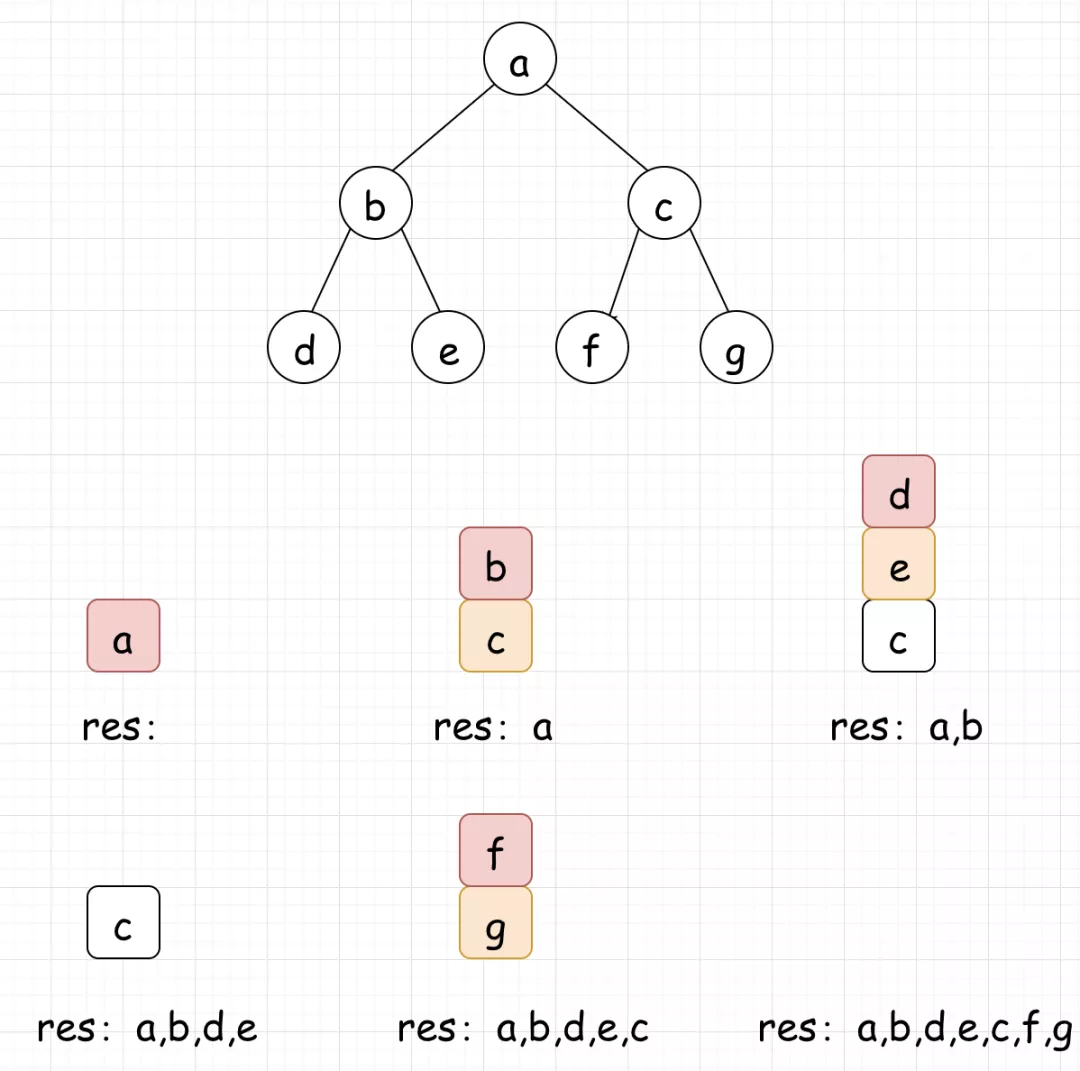
1:首先将a压入栈
2:a弹栈,将c、b压入栈(注意顺序)
3:b弹栈,将e、d压入栈
4:d、e、c弹栈,将g、f压入栈
5:f、g弹栈
至此,非递归的DFS就讲解完毕了。那我们如何通过非递归DFS的方式,来进行本题求解呢?相信已经很简单了,留下课后作业,请自行实践!
