判断回文链表

我们之前有两篇文章写了回文串和回文序列相关的问题。

寻找回文串的核心思想是从中心向两端扩展：

  1. string palindrome(string& s, int l, int r) {
  2.     // 防止索引越界
  3.     while (l >= 0 && r < s.size()
  4.             && s[l] == s[r]) {
  5.         // 向两边展开
  6.         l--; r++;
  7.     }
  8.     // 返回以 s[l] 和 s[r] 为中心的最长回文串
  9.     return s.substr(l + 1, r - l - 1);
  10. }

因为回文串长度可能为奇数也可能是偶数，长度为奇数时只存在一个中心点，而长度为偶数时存在两个中心点，所以上面这个函数需要传入l和r。

而判断一个字符串是不是回文串就简单很多，不需要考虑奇偶情况，只需要「双指针技巧」，从两端向中间逼近即可：

  1. bool isPalindrome(string s) {
  2.     int left = 0, right = s.length - 1;
  3.     while (left < right) {
  4.         if (s[left] != s[right])
  5.             return false;
  6.         left++; right--;
  7.     }
  8.     return true;
  9. }

以上代码很好理解吧，因为回文串是对称的，所以正着读和倒着读应该是一样的，这一特点是解决回文串问题的关键。

下面扩展这一最简单的情况，来解决：如何判断一个「单链表」是不是回文。

一、判断回文单链表

输入一个单链表的头结点，判断这个链表中的数字是不是回文：

  1. /**
  2.  * 单链表节点的定义：
  3.  * public class ListNode {
  4.  *     int val;
  5.  *     ListNode next;
  6.  * }
  7.  */
  9. boolean isPalindrome(ListNode head);
  11. 输入: 1->2->null
  12. 输出: false
  14. 输入: 1->2->2->1->null
  15. 输出: true

这道题的关键在于，单链表无法倒着遍历，无法使用双指针技巧。那么最简单的办法就是，把原始链表反转存入一条新的链表，然后比较这两条链表是否相同。关于如何反转链表，可以参见前文「递归操作链表」。

其实，借助二叉树后序遍历的思路，不需要显式反转原始链表也可以倒序遍历链表，下面来具体聊聊。

对于二叉树的几种遍历方式，我们再熟悉不过了：

  1. void traverse(TreeNode root) {
  2.     // 前序遍历代码
  3.     traverse(root.left);
  4.     // 中序遍历代码
  5.     traverse(root.right);
  6.     // 后序遍历代码
  7. }

在「学习数据结构的框架思维」中说过，链表兼具递归结构，树结构不过是链表的衍生。那么，链表其实也可以有前序遍历和后序遍历：

  1. void traverse(ListNode head) {
  2.     // 前序遍历代码
  3.     traverse(head.next);
  4.     // 后序遍历代码
  5. }

这个框架有什么指导意义呢？如果我想正序打印链表中的val值，可以在前序遍历位置写代码；反之，如果想倒序遍历链表，就可以在后序遍历位置操作：

  1. /* 倒序打印单链表中的元素值 */
  2. void traverse(ListNode head) {
  3.     if (head == null) return;
  4.     traverse(head.next);
  5.     // 后序遍历代码
  6.     print(head.val);
  7. }

说到这了，其实可以稍作修改，模仿双指针实现回文判断的功能：

  1. // 左侧指针
  2. ListNode left;
  4. boolean isPalindrome(ListNode head) {
  5.     left = head;
  6.     return traverse(head);
  7. }
  9. boolean traverse(ListNode right) {
  10.     if (right == null) return true;
  11.     boolean res = traverse(right.next);
  12.     // 后序遍历代码
  13.     res = res && (right.val == left.val);
  14.     left = left.next;
  15.     return res;
  16. }

这么做的核心逻辑是什么呢？实际上就是把链表节点放入一个栈，然后再拿出来，这时候元素顺序就是反的，只不过我们利用的是递归函数的堆栈而已。

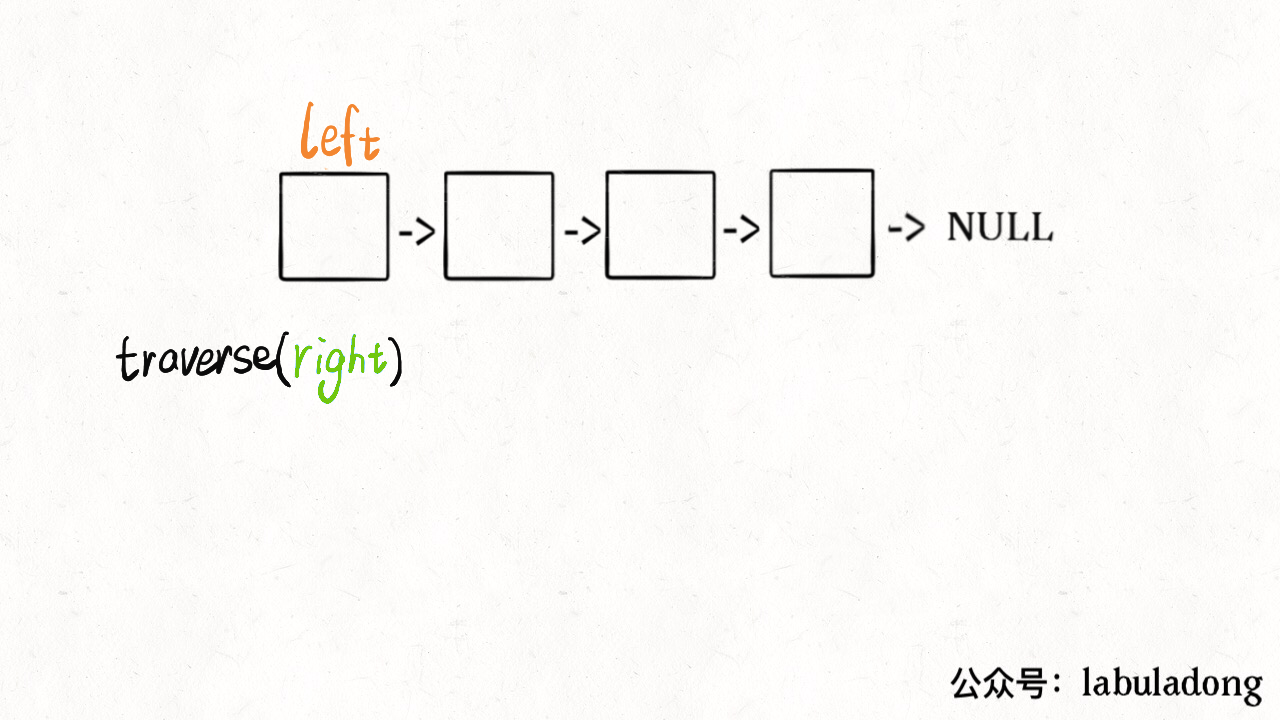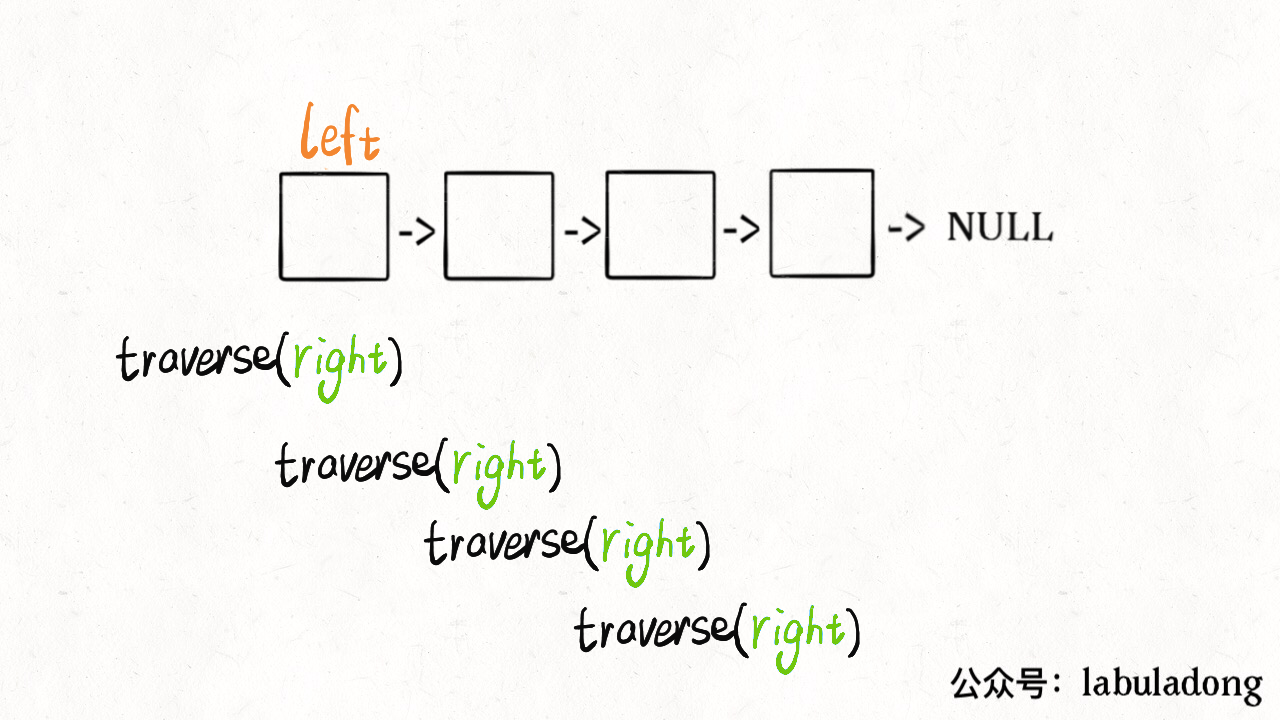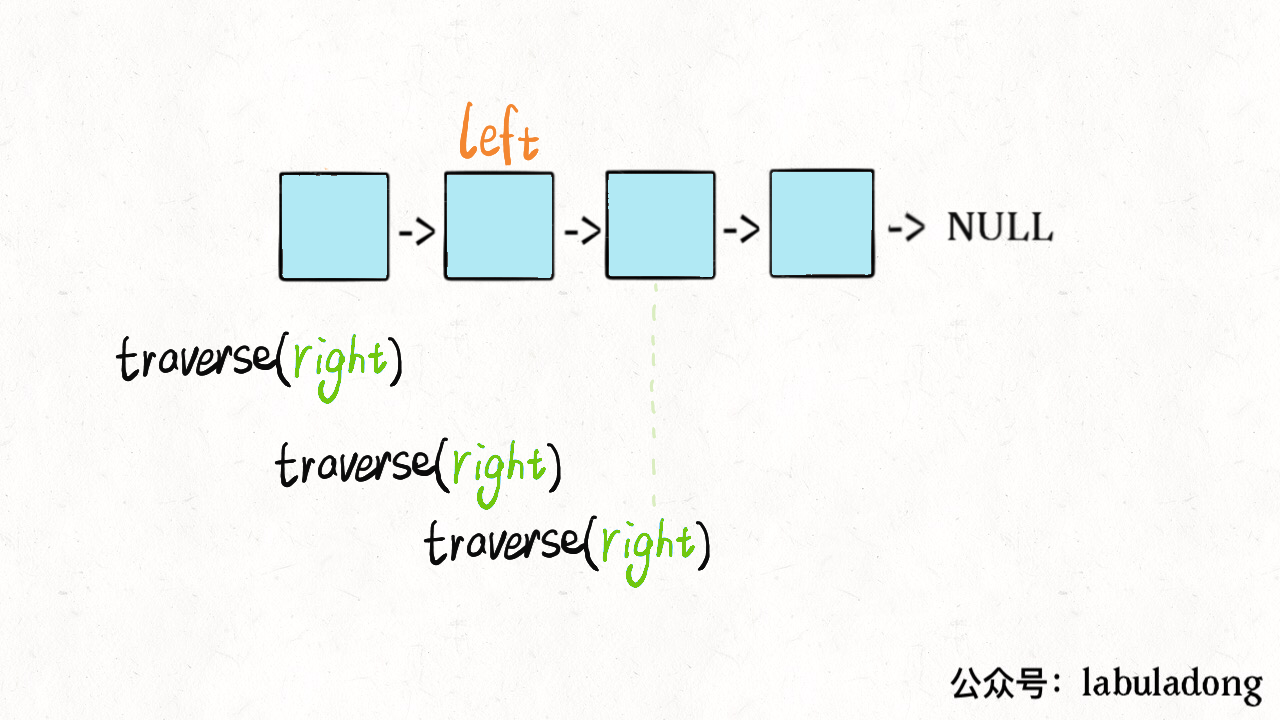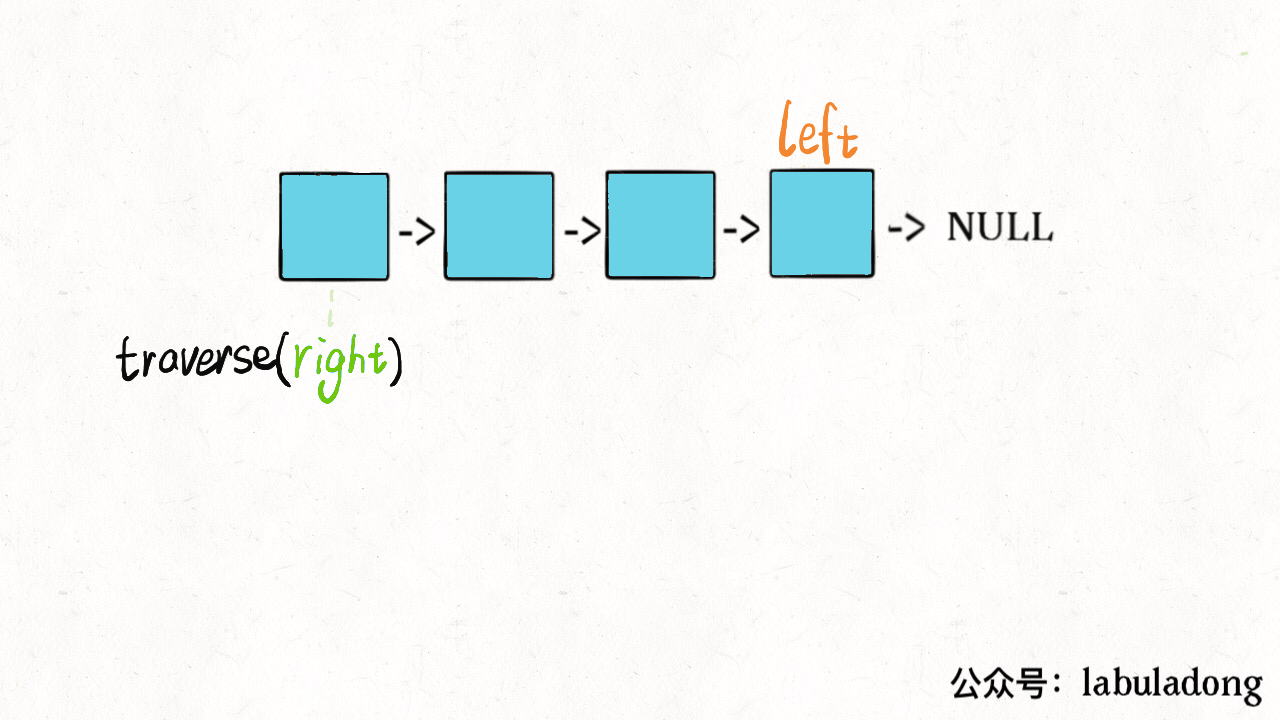
判断回文链表 - 图1

当然，无论造一条反转链表还是利用后续遍历，算法的时间和空间复杂度都是 O(N)。下面我们想想，能不能不用额外的空间，解决这个问题呢？

二、优化空间复杂度

更好的思路是这样的：

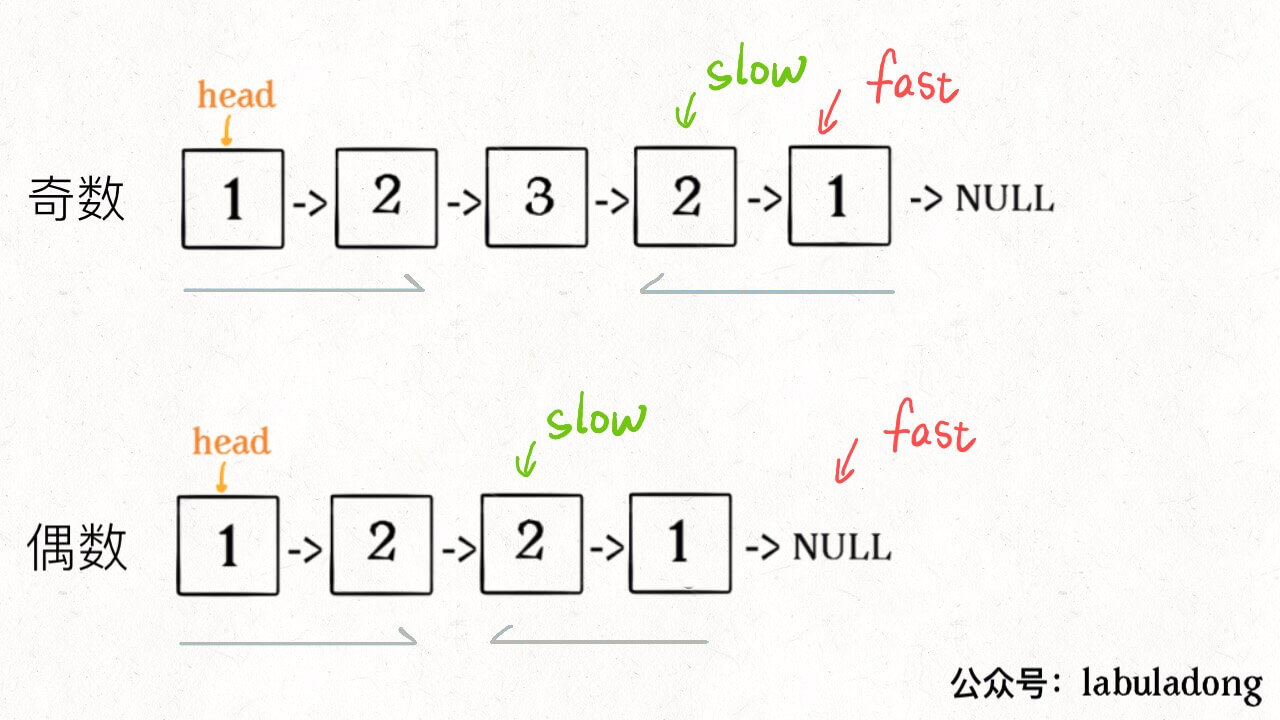
1、先通过「双指针技巧」中的快慢指针来找到链表的中点：

  1. ListNode slow, fast;
  2. slow = fast = head;
  3. while (fast != null && fast.next != null) {
  4.     slow = slow.next;
  5.     fast = fast.next.next;
  6. }
  7. // slow 指针现在指向链表中点

判断回文链表 - 图2

2、如果fast指针没有指向null，说明链表长度为奇数，slow还要再前进一步：

  1. if (fast != null)
  2.     slow = slow.next;

判断回文链表 - 图3

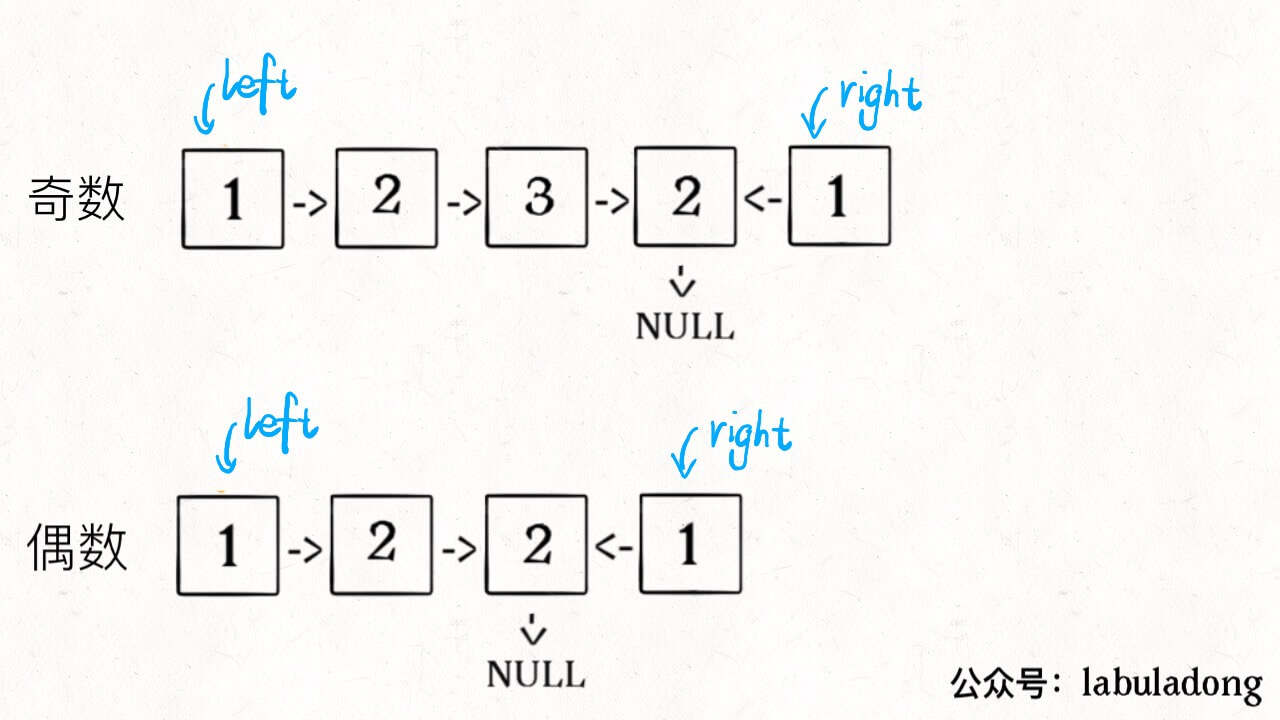
3、从slow开始反转后面的链表，现在就可以开始比较回文串了：

  1. ListNode left = head;
  2. ListNode right = reverse(slow);
  4. while (right != null) {
  5.     if (left.val != right.val)
  6.         return false;
  7.     left = left.next;
  8.     right = right.next;
  9. }
  10. return true;

判断回文链表 - 图4

至此，把上面 3 段代码合在一起就高效地解决这个问题了，其中reverse函数很容易实现：

  1. ListNode reverse(ListNode head) {
  2.     ListNode pre = null, cur = head;
  3.     while (cur != null) {
  4.         ListNode next = cur.next;
  5.         cur.next = pre;
  6.         pre = cur;
  7.         cur = next;
  8.     }
  9.     return pre;
  10. }

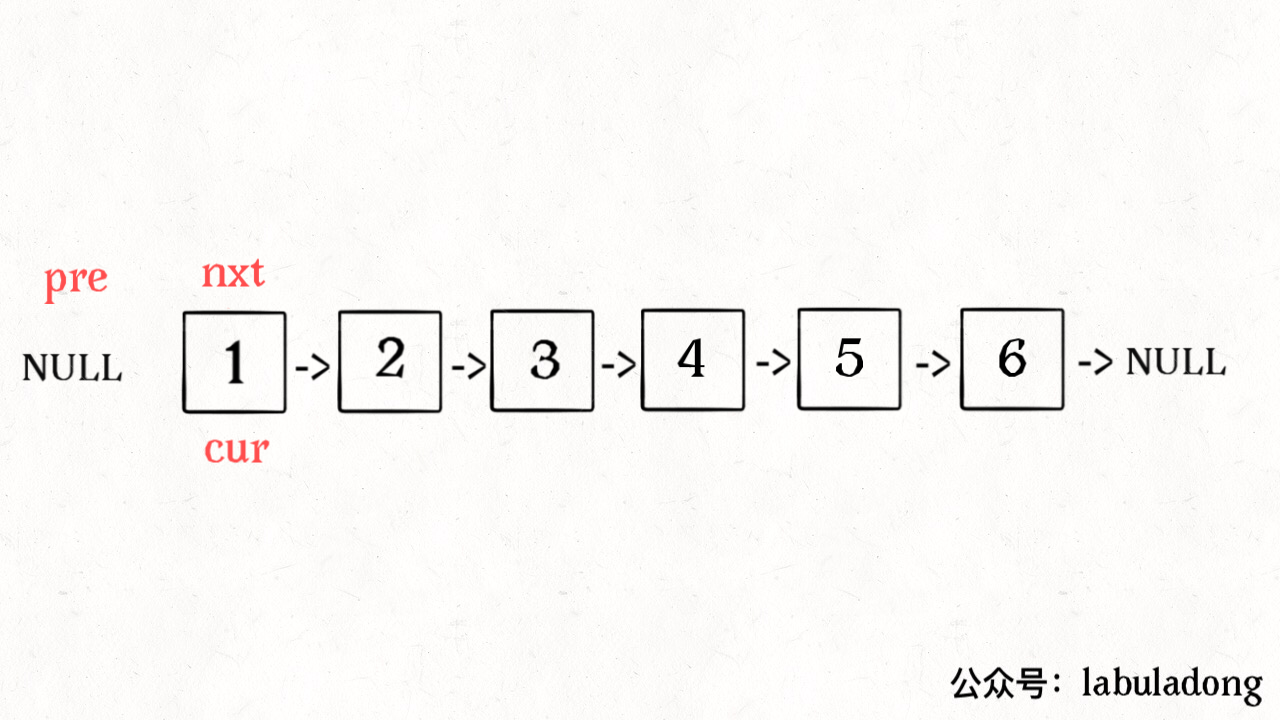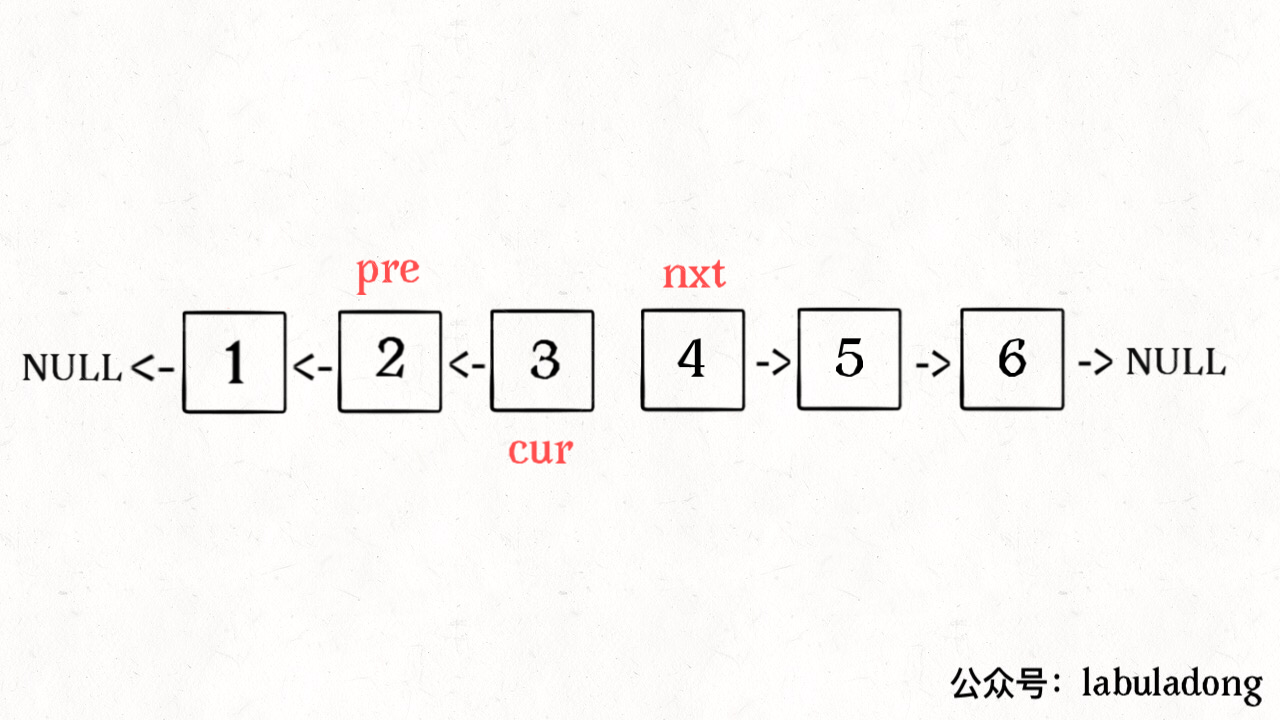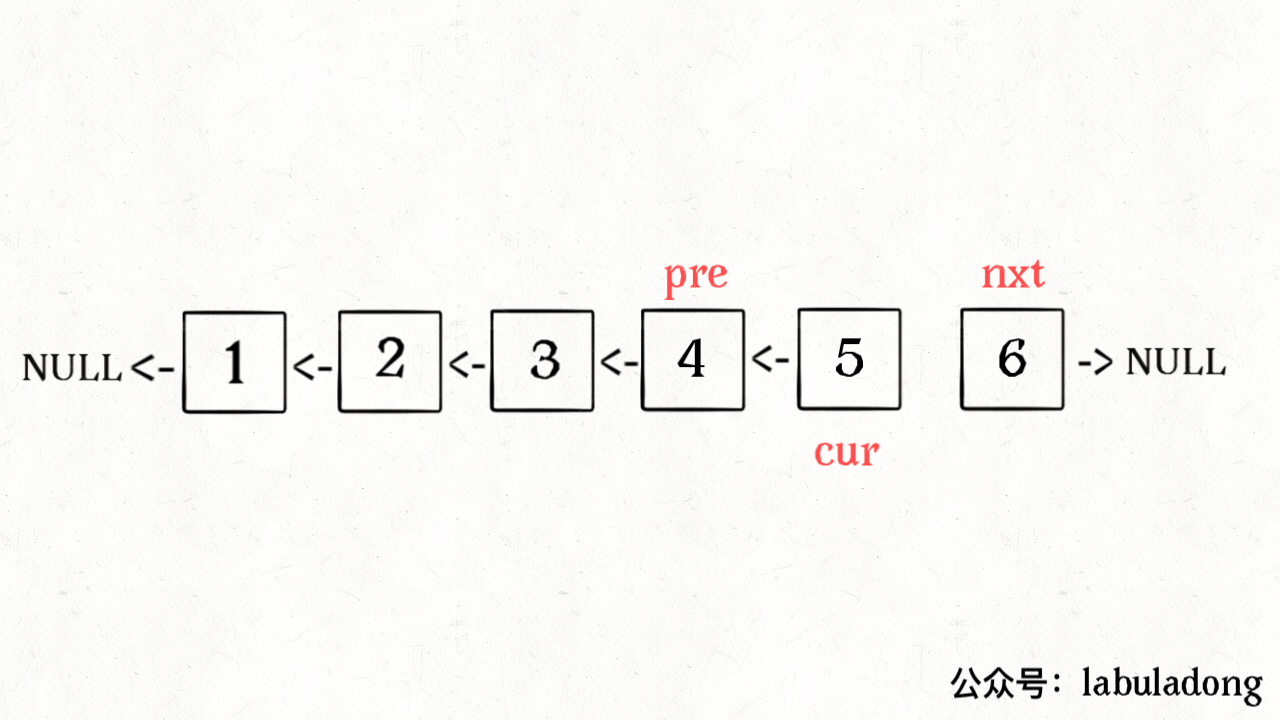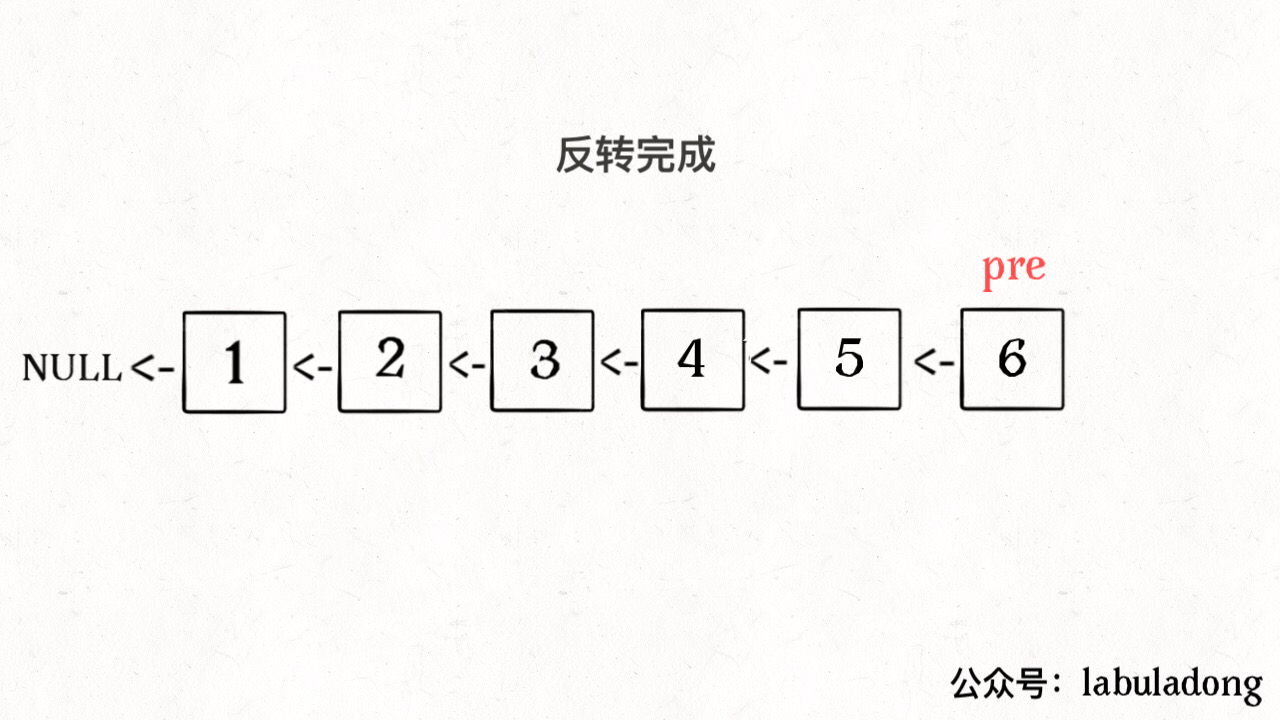
判断回文链表 - 图5

算法总体的时间复杂度 O(N)，空间复杂度 O(1)，已经是最优的了。

我知道肯定有读者会问：这种解法虽然高效，但破坏了输入链表的原始结构，能不能避免这个瑕疵呢？

其实这个问题很好解决，关键在于得到p, q这两个指针位置：

判断回文链表 - 图6

这样，只要在函数 return 之前加一段代码即可恢复原先链表顺序：

  1. p.next = reverse(q);

篇幅所限，我就不写了，读者可以自己尝试一下。

三、最后总结

首先，寻找回文串是从中间向两端扩展，判断回文串是从两端向中间收缩。对于单链表，无法直接倒序遍历，可以造一条新的反转链表，可以利用链表的后序遍历，也可以用栈结构倒序处理单链表。

具体到回文链表的判断问题，由于回文的特殊性，可以不完全反转链表，而是仅仅反转部分链表，将空间复杂度降到 O(1)。