队列实现栈|栈实现队列

队列是一种先进先出的数据结构，栈是一种先进后出的数据结构，形象一点就是这样：

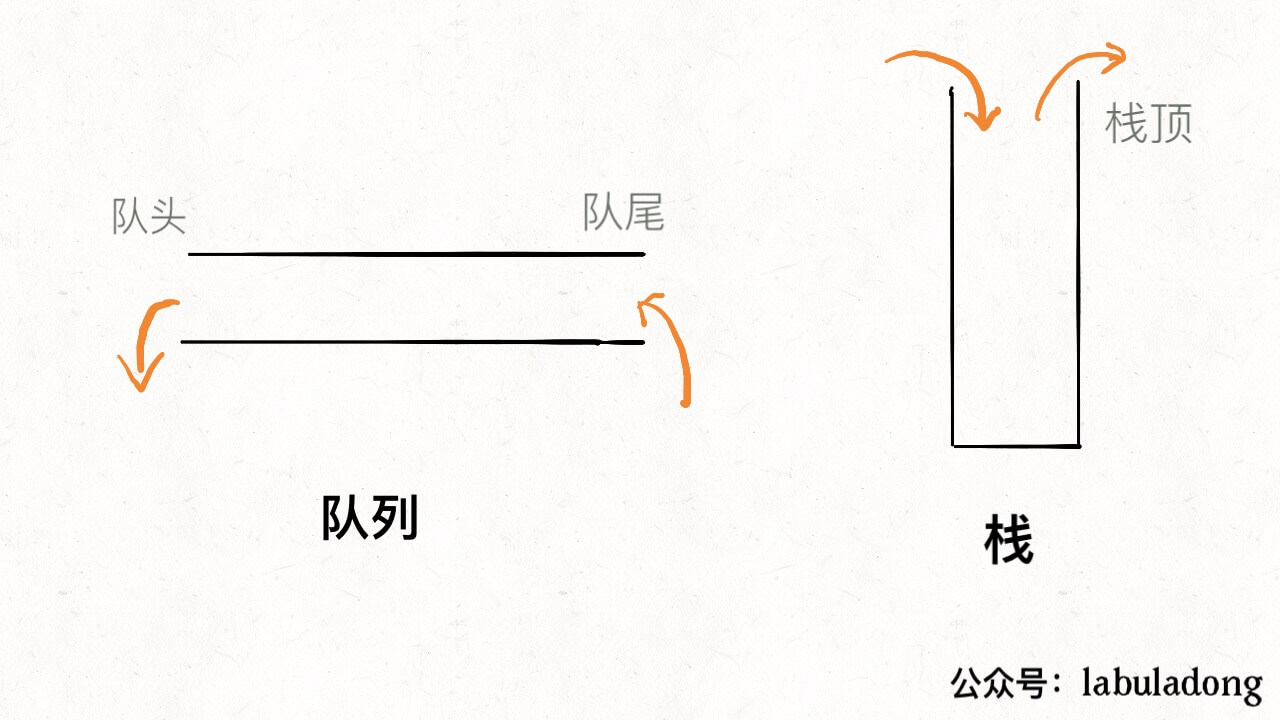
这两种数据结构底层其实都是数组或者链表实现的，只是 API 限定了它们的特性，那么今天就来看看如何使用「栈」的特性来实现一个「队列」，如何用「队列」实现一个「栈」。

一、用栈实现队列

首先，队列的 API 如下：

class MyQueue {
    /** 添加元素到队尾 */
    public void push(int x);
    /** 删除队头的元素并返回 */
    public int pop();
    /** 返回队头元素 */
    public int peek();
    /** 判断队列是否为空 */
    public boolean empty();
}

我们使用两个栈 s1, s2 就能实现一个队列的功能（这样放置栈可能更容易理解）：

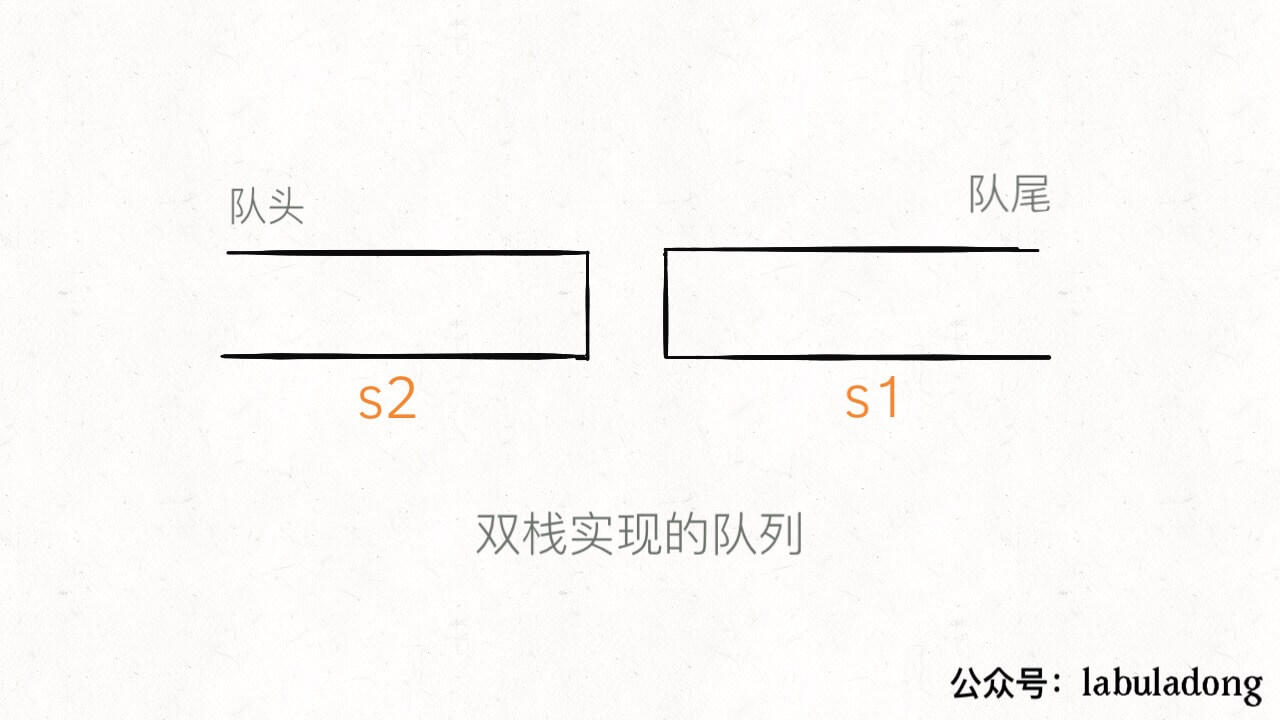
class MyQueue {
    private Stack<Integer> s1, s2;
    public MyQueue() {
        s1 = new Stack<>();
        s2 = new Stack<>();
    }
    // ...
}

当调用 push 让元素入队时，只要把元素压入 s1 即可，比如说 push 进 3 个元素分别是 1,2,3，那么底层结构就是这样：

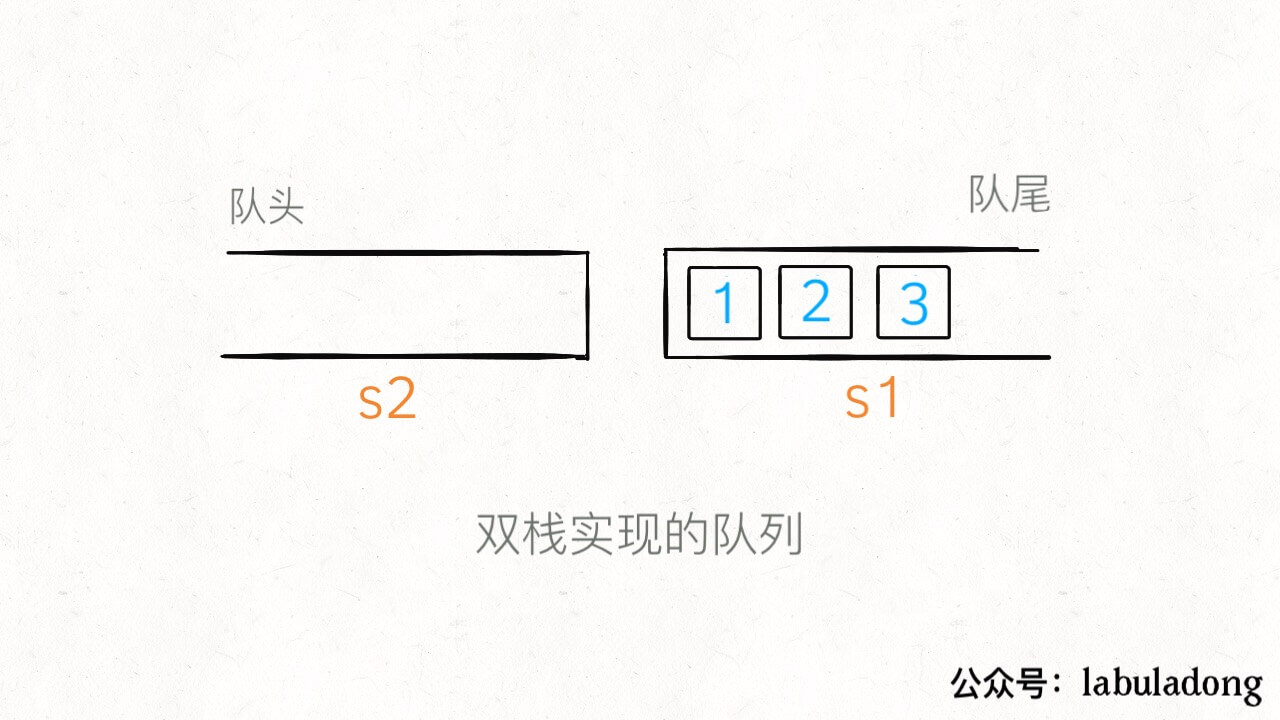
/** 添加元素到队尾 */
public void push(int x) {
    s1.push(x);
}

那么如果这时候使用 peek 查看队头的元素怎么办呢？按道理队头元素应该是 1，但是在 s1 中 1 被压在栈底，现在就要轮到 s2 起到一个中转的作用了：当 s2 为空时，可以把 s1 的所有元素取出再添加进 s2，这时候 s2 中元素就是先进先出顺序了。

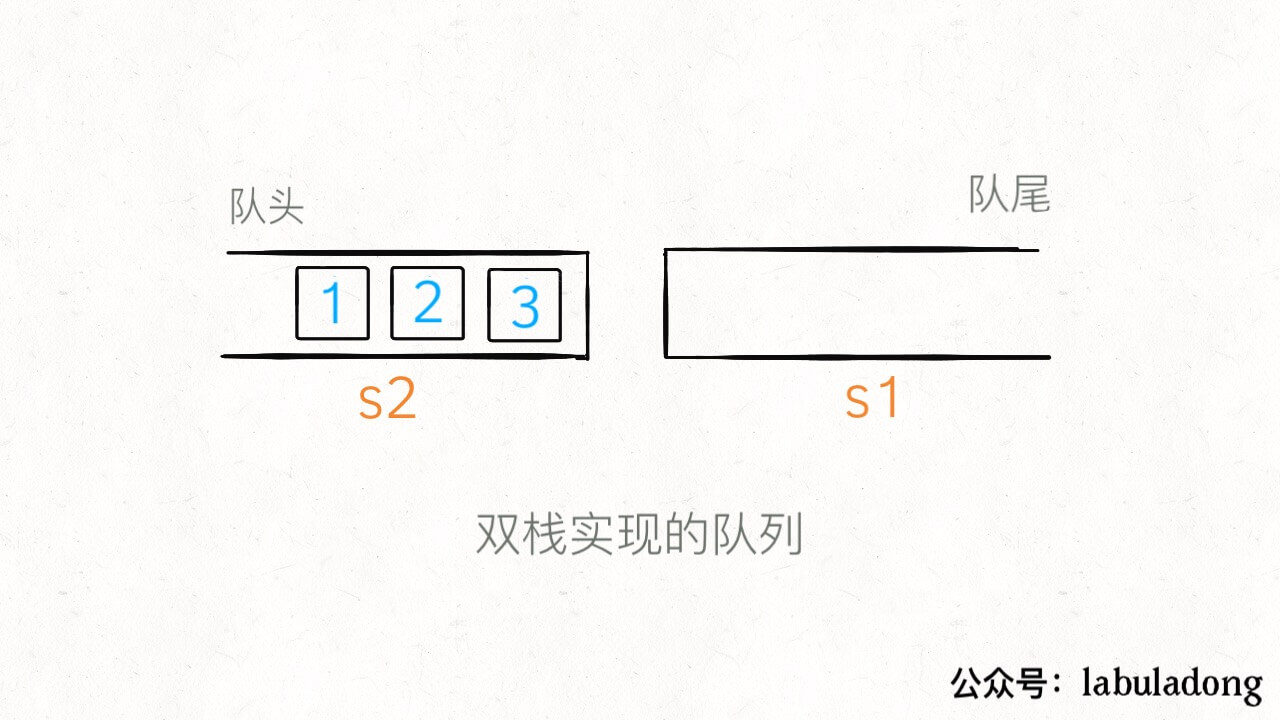
/** 返回队头元素 */
public int peek() {
    if (s2.isEmpty())
        // 把 s1 元素压入 s2
        while (!s1.isEmpty())
            s2.push(s1.pop());
    return s2.peek();
}

同理，对于 pop 操作，只要操作 s2 就可以了。

/** 删除队头的元素并返回 */
public int pop() {
    // 先调用 peek 保证 s2 非空
    peek();
    return s2.pop();
}

最后，如何判断队列是否为空呢？如果两个栈都为空的话，就说明队列为空：

/** 判断队列是否为空 */
public boolean empty() {
    return s1.isEmpty() && s2.isEmpty();
}

至此，就用栈结构实现了一个队列，核心思想是利用两个栈互相配合。

值得一提的是，这几个操作的时间复杂度是多少呢？有点意思的是 peek 操作，调用它时可能触发 while 循环，这样的话时间复杂度是 O(N)，但是大部分情况下 while 循环不会被触发，时间复杂度是 O(1)。由于 pop 操作调用了 peek，它的时间复杂度和 peek 相同。

像这种情况，可以说它们的最坏时间复杂度是 O(N)，因为包含 while 循环，可能需要从 s1 往 s2 搬移元素。

但是它们的均摊时间复杂度是 O(1)，这个要这么理解：对于一个元素，最多只可能被搬运一次，也就是说 peek 操作平均到每个元素的时间复杂度是 O(1)。

二、用队列实现栈

如果说双栈实现队列比较巧妙，那么用队列实现栈就比较简单粗暴了，只需要一个队列作为底层数据结构。首先看下栈的 API：

class MyStack {
    /** 添加元素到栈顶 */
    public void push(int x);
    /** 删除栈顶的元素并返回 */
    public int pop();
    /** 返回栈顶元素 */
    public int top();
    /** 判断栈是否为空 */
    public boolean empty();
}

先说 push API，直接将元素加入队列，同时记录队尾元素，因为队尾元素相当于栈顶元素，如果要 top 查看栈顶元素的话可以直接返回：

class MyStack {
    Queue<Integer> q = new LinkedList<>();
    int top_elem = 0;
    /** 添加元素到栈顶 */
    public void push(int x) {
        // x 是队列的队尾，是栈的栈顶
        q.offer(x);
        top_elem = x;
    }
    /** 返回栈顶元素 */
    public int top() {
        return top_elem;
    }
}

我们的底层数据结构是先进先出的队列，每次 pop 只能从队头取元素；但是栈是后进先出，也就是说 pop API 要从队尾取元素。

解决方法简单粗暴，把队列前面的都取出来再加入队尾，让之前的队尾元素排到队头，这样就可以取出了：

/** 删除栈顶的元素并返回 */
public int pop() {
    int size = q.size();
    while (size > 1) {
        q.offer(q.poll());
        size--;
    }
    // 之前的队尾元素已经到了队头
    return q.poll();
}

这样实现还有一点小问题就是，原来的队尾元素被提到队头并删除了，但是 top_elem 变量没有更新，我们还需要一点小修改：

/** 删除栈顶的元素并返回 */
public int pop() {
    int size = q.size();
    // 留下队尾 2 个元素
    while (size > 2) {
        q.offer(q.poll());
        size--;
    }
    // 记录新的队尾元素
    top_elem = q.peek();
    q.offer(q.poll());
    // 删除之前的队尾元素
    return q.poll();
}

最后，API empty 就很容易实现了，只要看底层的队列是否为空即可：

/** 判断栈是否为空 */
public boolean empty() {
    return q.isEmpty();
}

很明显，用队列实现栈的话，pop 操作时间复杂度是 O(N)，其他操作都是 O(1)​。​

个人认为，用队列实现栈是没啥亮点的问题，但是用双栈实现队列是值得学习的。

从栈 s1 搬运元素到 s2 之后，元素在 s2 中就变成了队列的先进先出顺序，这个特性有点类似「负负得正」，确实不太容易想到。

希望本文对你有帮助。

坚持原创高质量文章，致力于把算法问题讲清楚，欢迎关注我的公众号 labuladong 获取最新文章：

Xingsheng Qi 提供 用栈实现队列 C++解法代码：

class MyQueue {
private:
    stack<int> s1; 
    stack<int> s2;  
public:
    MyQueue() {
    }
    /** 添加元素到队尾 */
    void push(int x) {
        s1.push(x);
    }
    /** 删除队头的元素并返回 */
    int pop() {
        // 先调用 peek 保证 s2 非空
        peek();
        //保存 s2 的栈顶元素用于返回
        int tmp = s2.top();
        s2.pop();
        return tmp;
    }
    /** 返回队头元素 */
    int peek() {
        if (s2.empty())
        // 把 s1 元素压入 s2
            while (!s1.empty()){
                s2.push(s1.top());
                s1.pop();
            }
        return s2.top();
    }
    /** 判断队列是否为空 */
    bool empty() {
        return s1.empty()&& s2.empty();
    }
};

Xingsheng Qi 提供 用队列实现栈 C++解法代码：

class MyStack {
private:
    queue<int>q;
    int top_elem = 0;
public:
    MyStack() {
    }
    /** 添加元素到栈顶 */
    void push(int x) {
        // x 是队列的队尾，是栈的栈顶
        q.push(x);
        top_elem = x;
    }
    /** 删除栈顶的元素并返回 */
    int pop() {
        int size = q.size();
        // 留下队尾 2 个元素
        while (size > 2) {
            q.push(q.front());
            q.pop();
            size--;
        }
        // 记录新的队尾元素
        top_elem = q.front();
        q.push(q.front());
        q.pop();
        // 删除之前的队尾元素
        int tmp = q.front();
        q.pop();
        return tmp;
    }
    /** 返回栈顶元素 */
    int top() {
        return top_elem;
    }
    /** 判断栈是否为空 */
    bool empty() {
        return q.empty();
    }
};