经典动态规划问题:高楼扔鸡蛋
今天要聊一个很经典的算法问题,若干层楼,若干个鸡蛋,让你算出最少的尝试次数,找到鸡蛋恰好摔不碎的那层楼。国内大厂以及谷歌脸书面试都经常考察这道题,只不过他们觉得扔鸡蛋太浪费,改成扔杯子,扔破碗什么的。
具体的问题等会再说,但是这道题的解法技巧很多,光动态规划就好几种效率不同的思路,最后还有一种极其高效数学解法。秉承咱们号一贯的作风,拒绝奇技淫巧,拒绝过于诡异的技巧,因为这些技巧无法举一反三,学了也不划算。
下面就来用我们一直强调的动态规划通用思路来研究一下这道题。
一、解析题目
题目是这样:你面前有一栋从 1 到 N 共 N 层的楼,然后给你 K 个鸡蛋(K 至少为 1)。现在确定这栋楼存在楼层 0 <= F <= N,在这层楼将鸡蛋扔下去,鸡蛋恰好没摔碎(高于 F 的楼层都会碎,低于 F 的楼层都不会碎)。现在问你,最坏情况下,你至少要扔几次鸡蛋,才能确定这个楼层 F 呢?
也就是让你找摔不碎鸡蛋的最高楼层 F,但什么叫「最坏情况」下「至少」要扔几次呢?我们分别举个例子就明白了。
比方说现在先不管鸡蛋个数的限制,有 7 层楼,你怎么去找鸡蛋恰好摔碎的那层楼?
最原始的方式就是线性扫描:我先在 1 楼扔一下,没碎,我再去 2 楼扔一下,没碎,我再去 3 楼……
以这种策略,最坏情况应该就是我试到第 7 层鸡蛋也没碎(F = 7),也就是我扔了 7 次鸡蛋。
先在你应该理解什么叫做「最坏情况」下了,鸡蛋破碎一定发生在搜索区间穷尽时,不会说你在第 1 层摔一下鸡蛋就碎了,这是你运气好,不是最坏情况。
现在再来理解一下什么叫「至少」要扔几次。依然不考虑鸡蛋个数限制,同样是 7 层楼,我们可以优化策略。
最好的策略是使用二分查找思路,我先去第 (1 + 7) / 2 = 4 层扔一下:
如果碎了说明 F 小于 4,我就去第 (1 + 3) / 2 = 2 层试……
如果没碎说明 F 大于等于 4,我就去第 (5 + 7) / 2 = 6 层试……
以这种策略,最坏情况应该是试到第 7 层鸡蛋还没碎(F = 7),或者鸡蛋一直碎到第 1 层(F = 0)。然而无论那种最坏情况,只需要试 log7 向上取整等于 3 次,比刚才尝试 7 次要少,这就是所谓的至少要扔几次。
PS:这有点像 Big O 表示法计算算法的复杂度。
实际上,如果不限制鸡蛋个数的话,二分思路显然可以得到最少尝试的次数,但问题是,现在给你了鸡蛋个数的限制 K,直接使用二分思路就不行了。
比如说只给你 1 个鸡蛋,7 层楼,你敢用二分吗?你直接去第 4 层扔一下,如果鸡蛋没碎还好,但如果碎了你就没有鸡蛋继续测试了,无法确定鸡蛋恰好摔不碎的楼层 F 了。这种情况下只能用线性扫描的方法,算法返回结果应该是 7。
有的读者也许会有这种想法:二分查找排除楼层的速度无疑是最快的,那干脆先用二分查找,等到只剩 1 个鸡蛋的时候再执行线性扫描,这样得到的结果是不是就是最少的扔鸡蛋次数呢?
很遗憾,并不是,比如说把楼层变高一些,100 层,给你 2 个鸡蛋,你在 50 层扔一下,碎了,那就只能线性扫描 1~49 层了,最坏情况下要扔 50 次。
如果不要「二分」,变成「五分」「十分」都会大幅减少最坏情况下的尝试次数。比方说第一个鸡蛋每隔十层楼扔,在哪里碎了第二个鸡蛋一个个线性扫描,总共不会超过 20 次。
最优解其实是 14 次。最优策略非常多,而且并没有什么规律可言。
说了这么多废话,就是确保大家理解了题目的意思,而且认识到这个题目确实复杂,就连我们手算都不容易,如何用算法解决呢?
二、思路分析
对动态规划问题,直接套我们以前多次强调的框架即可:这个问题有什么「状态」,有什么「选择」,然后穷举。
「状态」很明显,就是当前拥有的鸡蛋数 K 和需要测试的楼层数 N。随着测试的进行,鸡蛋个数可能减少,楼层的搜索范围会减小,这就是状态的变化。
「选择」其实就是去选择哪层楼扔鸡蛋。回顾刚才的线性扫描和二分思路,二分查找每次选择到楼层区间的中间去扔鸡蛋,而线性扫描选择一层层向上测试。不同的选择会造成状态的转移。
现在明确了「状态」和「选择」,动态规划的基本思路就形成了:肯定是个二维的 dp 数组或者带有两个状态参数的 dp 函数来表示状态转移;外加一个 for 循环来遍历所有选择,择最优的选择更新状态:
# 当前状态为 K 个鸡蛋,面对 N 层楼# 返回这个状态下的最优结果def dp(K, N):int resfor 1 <= i <= N:res = min(res, 这次在第 i 层楼扔鸡蛋)return res
这段伪码还没有展示递归和状态转移,不过大致的算法框架已经完成了。
我们选择在第 i 层楼扔了鸡蛋之后,可能出现两种情况:鸡蛋碎了,鸡蛋没碎。注意,这时候状态转移就来了:
如果鸡蛋碎了,那么鸡蛋的个数 K 应该减一,搜索的楼层区间应该从 [1..N] 变为 [1..i-1] 共 i-1 层楼;
如果鸡蛋没碎,那么鸡蛋的个数 K 不变,搜索的楼层区间应该从 [1..N] 变为 [i+1..N] 共 N-i 层楼。
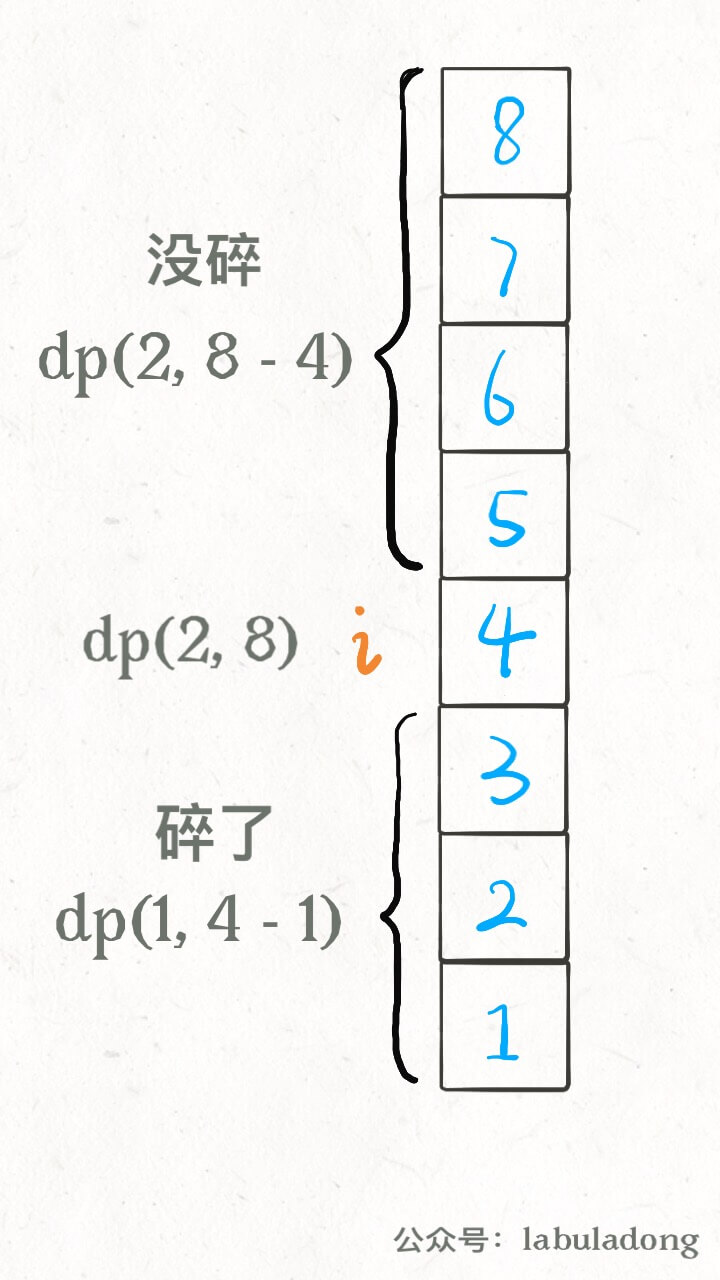
PS:细心的读者可能会问,在第i层楼扔鸡蛋如果没碎,楼层的搜索区间缩小至上面的楼层,是不是应该包含第i层楼呀?不必,因为已经包含了。开头说了 F 是可以等于 0 的,向上递归后,第i层楼其实就相当于第 0 层,可以被取到,所以说并没有错误。
因为我们要求的是最坏情况下扔鸡蛋的次数,所以鸡蛋在第 i 层楼碎没碎,取决于那种情况的结果更大:
def dp(K, N):for 1 <= i <= N:# 最坏情况下的最少扔鸡蛋次数res = min(res,max(dp(K - 1, i - 1), # 碎dp(K, N - i) # 没碎) + 1 # 在第 i 楼扔了一次)return res
递归的 base case 很容易理解:当楼层数 N 等于 0 时,显然不需要扔鸡蛋;当鸡蛋数 K 为 1 时,显然只能线性扫描所有楼层:
def dp(K, N):if K == 1: return Nif N == 0: return 0...
至此,其实这道题就解决了!只要添加一个备忘录消除重叠子问题即可:
def superEggDrop(K: int, N: int):memo = dict()def dp(K, N) -> int:# base caseif K == 1: return Nif N == 0: return 0# 避免重复计算if (K, N) in memo:return memo[(K, N)]res = float('INF')# 穷举所有可能的选择for i in range(1, N + 1):res = min(res,max(dp(K, N - i),dp(K - 1, i - 1)) + 1)# 记入备忘录memo[(K, N)] = resreturn resreturn dp(K, N)
这个算法的时间复杂度是多少呢?动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度。
函数本身的复杂度就是忽略递归部分的复杂度,这里 dp 函数中有一个 for 循环,所以函数本身的复杂度是 O(N)。
子问题个数也就是不同状态组合的总数,显然是两个状态的乘积,也就是 O(KN)。
所以算法的总时间复杂度是 O(K*N^2), 空间复杂度 O(KN)。
三、疑难解答
这个问题很复杂,但是算法代码却十分简洁,这就是动态规划的特性,穷举加备忘录/DP table 优化,真的没啥新意。
首先,有读者可能不理解代码中为什么用一个 for 循环遍历楼层 [1..N],也许会把这个逻辑和之前探讨的线性扫描混为一谈。其实不是的,这只是在做一次「选择」。
比方说你有 2 个鸡蛋,面对 10 层楼,你这次选择去哪一层楼扔呢?不知道,那就把这 10 层楼全试一遍。至于下次怎么选择不用你操心,有正确的状态转移,递归会算出每个选择的代价,我们取最优的那个就是最优解。
另外,这个问题还有更好的解法,比如修改代码中的 for 循环为二分搜索,可以将时间复杂度降为 O(K*N*logN);再改进动态规划解法可以进一步降为 O(KN);使用数学方法解决,时间复杂度达到最优 O(K*logN),空间复杂度达到 O(1)。
二分的解法也有点误导性,你很可能以为它跟我们之前讨论的二分思路扔鸡蛋有关系,实际上没有半毛钱关系。能用二分搜索是因为状态转移方程的函数图像具有单调性,可以快速找到最值。
简单介绍一下二分查找的优化吧,其实只是在优化这段代码:
def dp(K, N):for 1 <= i <= N:# 最坏情况下的最少扔鸡蛋次数res = min(res,max(dp(K - 1, i - 1), # 碎dp(K, N - i) # 没碎) + 1 # 在第 i 楼扔了一次)return res
这个 for 循环就是下面这个状态转移方程的具体代码实现:
首先我们根据 dp(K, N) 数组的定义(有 K 个鸡蛋面对 N 层楼,最少需要扔几次),很容易知道 K 固定时,这个函数一定是单调递增的,无论你策略多聪明,楼层增加测试次数一定要增加。
那么注意 dp(K - 1, i - 1) 和 dp(K, N - i) 这两个函数,其中 i 是从 1 到 N 单增的,如果我们固定 K 和 N,把这两个函数看做关于 i 的函数,前者随着 i 的增加应该也是单调递增的,而后者随着 i 的增加应该是单调递减的:
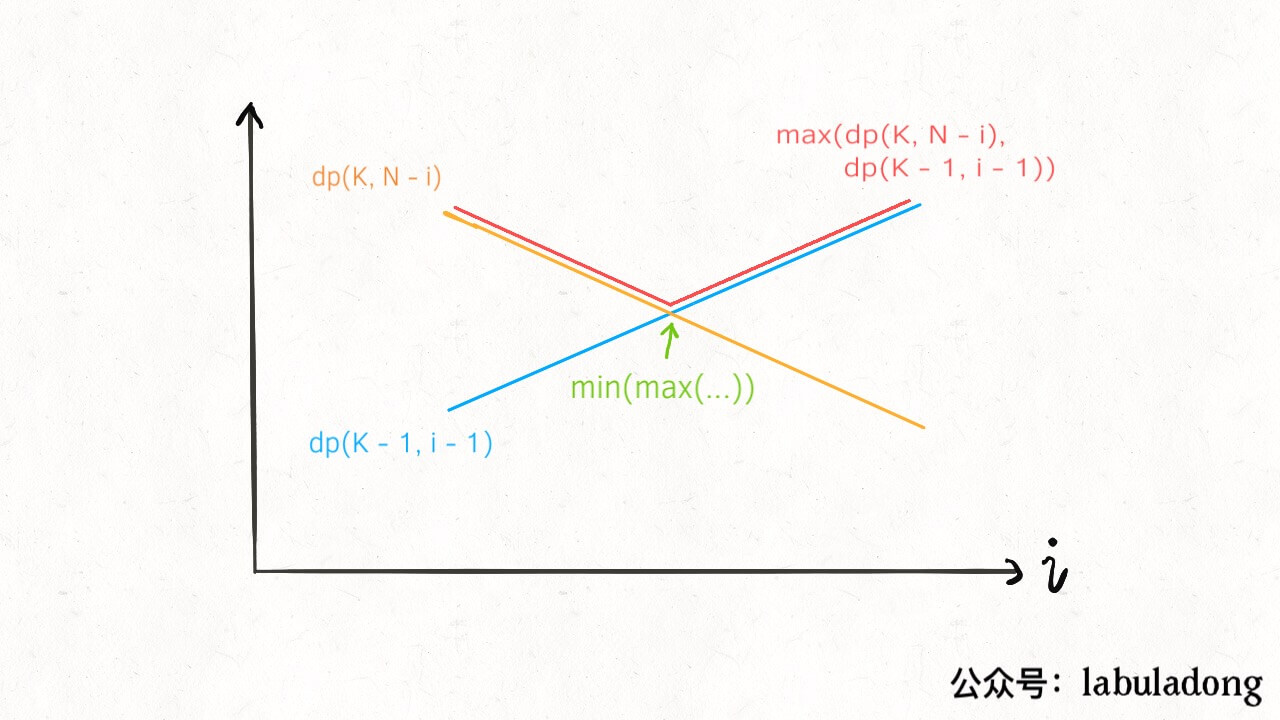
这时候求二者的较大值,再求这些最大值之中的最小值,其实就是求这个交点嘛,熟悉二分搜索的同学肯定敏感地想到了,这不就是相当于求 Valley(山谷)值嘛,可以用二分查找来快速寻找这个点的。
直接贴一下代码吧,思路还是完全一样的:
def superEggDrop(self, K: int, N: int) -> int:memo = dict()def dp(K, N):if K == 1: return Nif N == 0: return 0if (K, N) in memo:return memo[(K, N)]# for 1 <= i <= N:# res = min(res,# max(# dp(K - 1, i - 1),# dp(K, N - i)# ) + 1# )res = float('INF')# 用二分搜索代替线性搜索lo, hi = 1, Nwhile lo <= hi:mid = (lo + hi) // 2broken = dp(K - 1, mid - 1) # 碎not_broken = dp(K, N - mid) # 没碎# res = min(max(碎,没碎) + 1)if broken > not_broken:hi = mid - 1res = min(res, broken + 1)else:lo = mid + 1res = min(res, not_broken + 1)memo[(K, N)] = resreturn resreturn dp(K, N)
这里就不展开其他解法了,留在下一篇文章 高楼扔鸡蛋进阶
我觉得吧,我们这种解法就够了:找状态,做选择,足够清晰易懂,可流程化,可举一反三。掌握这套框架学有余力的话,再去考虑那些奇技淫巧也不迟。
最后预告一下,《动态规划详解(修订版)》和《回溯算法详解(修订版)》已经动笔了,教大家用模板的力量来对抗变化无穷的算法题,敬请期待。
致力于把算法讲清楚!欢迎关注我的微信公众号 labuladong,查看更多通俗易懂的文章:

renxiaoyao 提供C++解法代码: 1) 状态定义一:动态规划 + 二分查找
class Solution {public:int superEggDrop(int K,int N) {vector<vector<int>> dp(N + 1,vector<int>(K + 1,0));for(int j = 1 ; j <= K ; ++j)dp[1][j] = 1;for(int i = 1 ; i <= N ; ++i)dp[i][1] = i;for(int i = 2 ; i <= N ; ++i)for(int j = 2 ; j <= K ; ++j)dp[i][j] = binary_Valley(i,j,dp);return dp[N][K];}private:int binary_Valley(int floors,int eggs,vector<vector<int>>& dp) {int l = 1;int r = floors;while(l < r) {int LMid = l + (r - l) / 2;int broken = dp[LMid - 1][eggs - 1];int not_broken = dp[floors - LMid][eggs];if(not_broken > broken)l = LMid + 1;elser = LMid;}return max(dp[r - 1][eggs - 1],dp[floors - r][eggs]) + 1;}};
