动态规划之子序列问题解题模板

子序列问题是常见的算法问题，而且并不好解决。

首先，子序列问题本身就相对子串、子数组更困难一些，因为前者是不连续的序列，而后两者是连续的，就算穷举你都不一定会，更别说求解相关的算法问题了。

而且，子序列问题很可能涉及到两个字符串，比如前文「最长公共子序列」，如果没有一定的处理经验，真的不容易想出来。所以本文就来扒一扒子序列问题的套路，其实就有两种模板，相关问题只要往这两种思路上想，十拿九稳。

一般来说，这类问题都是让你求一个最长子序列，因为最短子序列就是一个字符嘛，没啥可问的。一旦涉及到子序列和最值，那几乎可以肯定，考察的是动态规划技巧，时间复杂度一般都是 O(n^2)。

原因很简单，你想想一个字符串，它的子序列有多少种可能？起码是指数级的吧，这种情况下，不用动态规划技巧，还想怎么着？

既然要用动态规划，那就要定义 dp 数组，找状态转移关系。我们说的两种思路模板，就是 dp 数组的定义思路。不同的问题可能需要不同的 dp 数组定义来解决。

一、两种思路

1、第一种思路模板是一个一维的 dp 数组：

  1. int n = array.length;
  2. int[] dp = new int[n];
  4. for (int i = 1; i < n; i++) {
  5.     for (int j = 0; j < i; j++) {
  6.         dp[i] = 最值(dp[i], dp[j] + ...)
  7.     }
  8. }

举个我们写过的例子「最长递增子序列」，在这个思路中 dp 数组的定义是：

在子数组 array[0..i] 中，我们要求的子序列（最长递增子序列）的长度是 dp[i]。

为啥最长递增子序列需要这种思路呢？前文说得很清楚了，因为这样符合归纳法，可以找到状态转移的关系，这里就不具体展开了。

2、第二种思路模板是一个二维的 dp 数组：

  1. int n = arr.length;
  2. int[][] dp = new int[n][n];
  4. for (int i = 0; i < n; i++) {
  5.     for (int j = 0; j < n; j++) {
  6.         if (arr[i] == arr[j]) 
  7.             dp[i][j] = dp[i][j] + ...
  8.         else
  9.             dp[i][j] = 最值(...)
  10.     }
  11. }

这种思路运用相对更多一些，尤其是涉及两个字符串/数组的子序列，比如前文讲的「最长公共子序列」。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。

2.1 涉及两个字符串/数组时（比如最长公共子序列），dp 数组的含义如下：

在子数组 arr1[0..i] 和子数组 arr2[0..j] 中，我们要求的子序列（最长公共子序列）长度为 dp[i][j]。

2.2 只涉及一个字符串/数组时（比如本文要讲的最长回文子序列），dp 数组的含义如下：

在子数组 array[i..j] 中，我们要求的子序列（最长回文子序列）的长度为 dp[i][j]。

第一种情况可以参考这两篇旧文：「编辑距离」「公共子序列」

下面就借最长回文子序列这个问题，详解一下第二种情况下如何使用动态规划。

二、最长回文子序列

之前解决了「最长回文子串」的问题，这次提升难度，求最长回文子序列的长度：

动态规划之子序列问题解题模板 - 图1

我们说这个问题对 dp 数组的定义是：在子串 s[i..j] 中，最长回文子序列的长度为 dp[i][j]。一定要记住这个定义才能理解算法。

为啥这个问题要这样定义二维的 dp 数组呢？我们前文多次提到，找状态转移需要归纳思维，说白了就是如何从已知的结果推出未知的部分，这样定义容易归纳，容易发现状态转移关系。

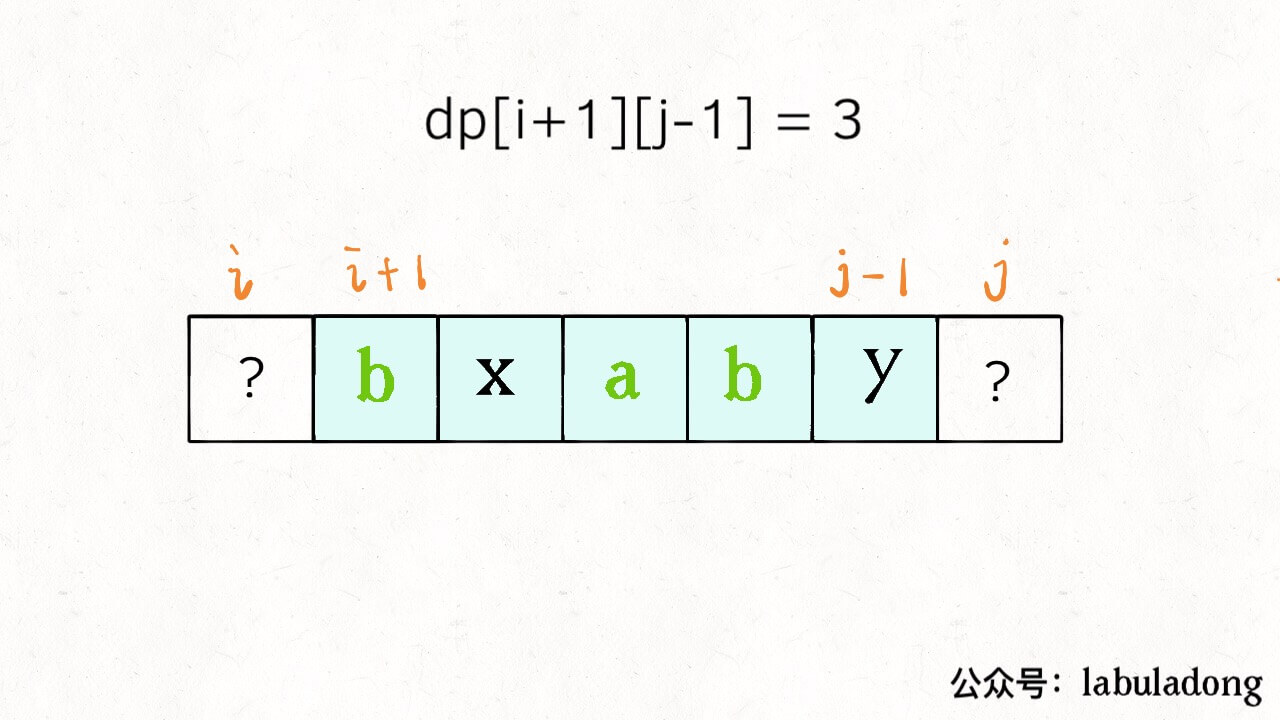
具体来说，如果我们想求 dp[i][j]，假设你知道了子问题 dp[i+1][j-1] 的结果（s[i+1..j-1] 中最长回文子序列的长度），你是否能想办法算出 dp[i][j] 的值（s[i..j] 中，最长回文子序列的长度）呢？

动态规划之子序列问题解题模板 - 图2

可以！这取决于 s[i] 和 s[j] 的字符：

如果它俩相等，那么它俩加上 s[i+1..j-1] 中的最长回文子序列就是 s[i..j] 的最长回文子序列：

动态规划之子序列问题解题模板 - 图3

如果它俩不相等，说明它俩不可能同时出现在 s[i..j] 的最长回文子序列中，那么把它俩分别加入 s[i+1..j-1] 中，看看哪个子串产生的回文子序列更长即可：

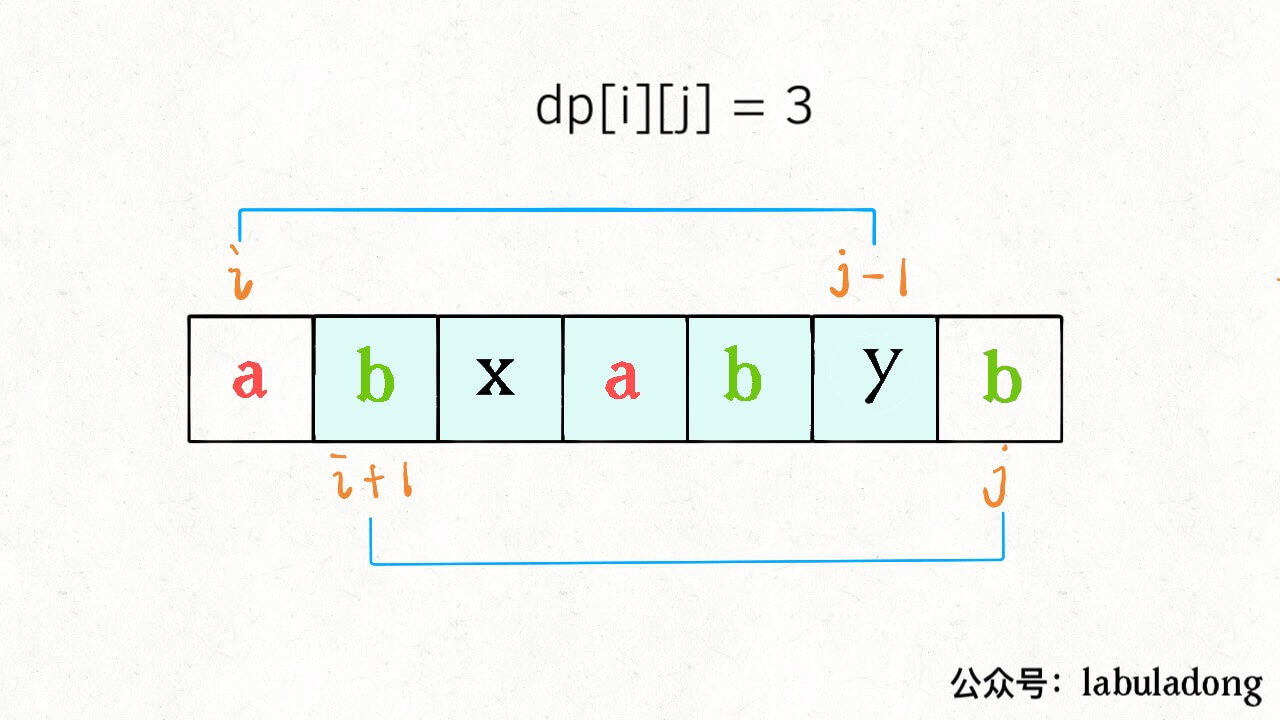
动态规划之子序列问题解题模板 - 图4

以上两种情况写成代码就是这样：

  1. if (s[i] == s[j])
  2.     // 它俩一定在最长回文子序列中
  3.     dp[i][j] = dp[i + 1][j - 1] + 2;
  4. else
  5.     // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
  6.     dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

至此，状态转移方程就写出来了，根据 dp 数组的定义，我们要求的就是 dp[0][n - 1]，也就是整个 s 的最长回文子序列的长度。

三、代码实现

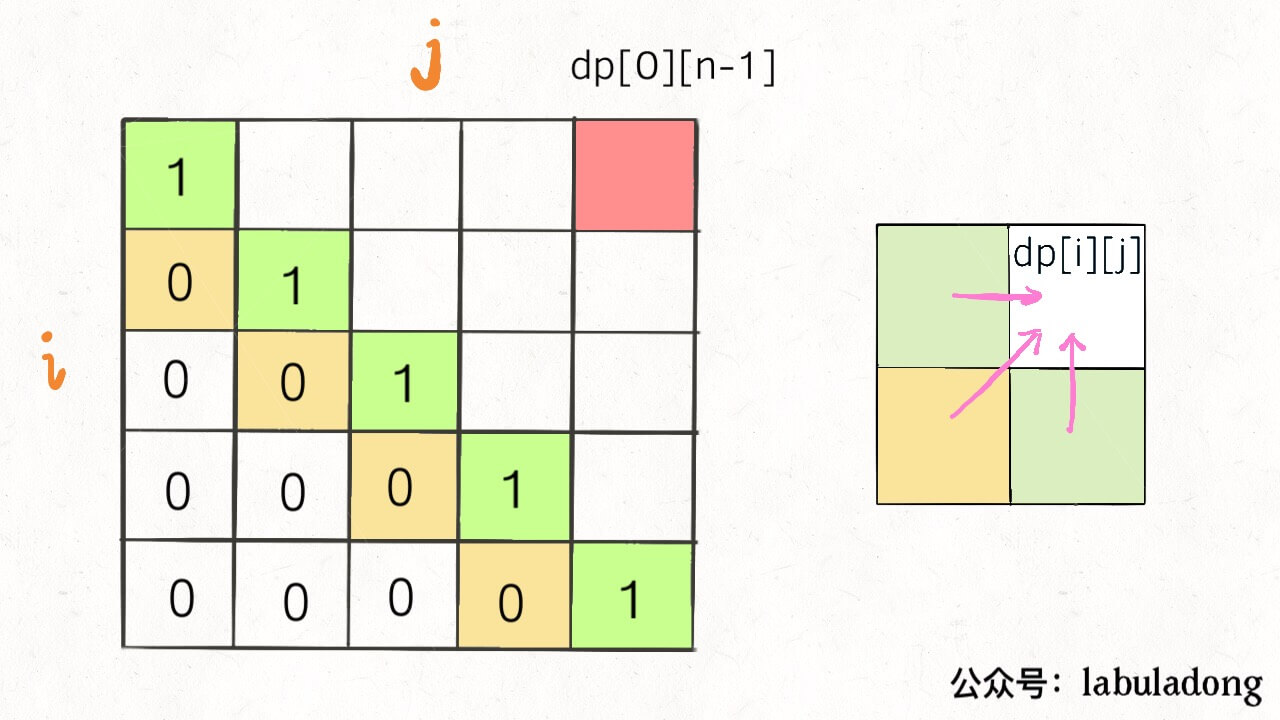
首先明确一下 base case，如果只有一个字符，显然最长回文子序列长度是 1，也就是 dp[i][j] = 1 (i == j)。

因为 i 肯定小于等于 j，所以对于那些 i > j 的位置，根本不存在什么子序列，应该初始化为 0。

另外，看看刚才写的状态转移方程，想求 dp[i][j] 需要知道 dp[i+1][j-1]，dp[i+1][j]，dp[i][j-1] 这三个位置；再看看我们确定的 base case，填入 dp 数组之后是这样：

动态规划之子序列问题解题模板 - 图5

为了保证每次计算 dp[i][j]，左下右方向的位置已经被计算出来，只能斜着遍历或者反着遍历：

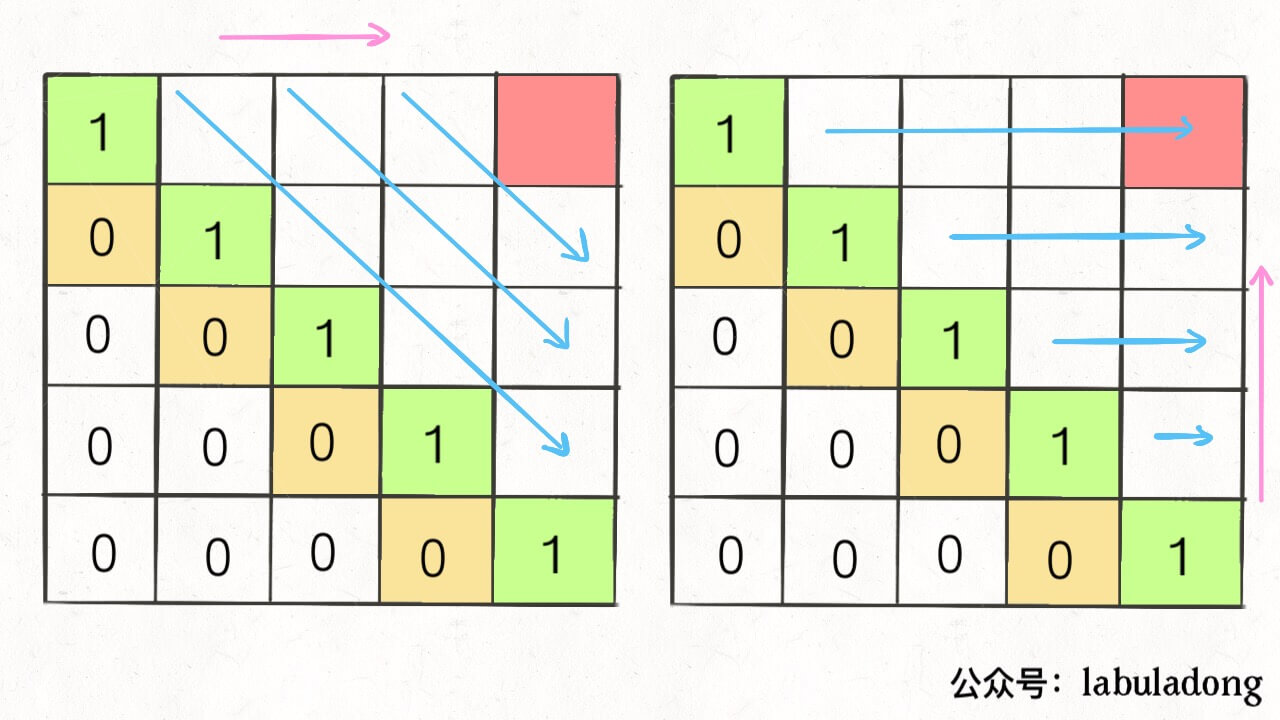
动态规划之子序列问题解题模板 - 图6

我选择反着遍历，代码如下：

  1. int longestPalindromeSubseq(string s) {
  2.     int n = s.size();
  3.     // dp 数组全部初始化为 0
  4.     vector<vector<int>> dp(n, vector<int>(n, 0));
  5.     // base case
  6.     for (int i = 0; i < n; i++)
  7.         dp[i][i] = 1;
  8.     // 反着遍历保证正确的状态转移
  9.     for (int i = n - 1; i >= 0; i--) {
  10.         for (int j = i + 1; j < n; j++) {
  11.             // 状态转移方程
  12.             if (s[i] == s[j])
  13.                 dp[i][j] = dp[i + 1][j - 1] + 2;
  14.             else
  15.                 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
  16.         }
  17.     }
  18.     // 整个 s 的最长回文子串长度
  19.     return dp[0][n - 1];
  20. }

至此，最长回文子序列的问题就解决了。