特殊数据结构：单调队列

前文讲了一种特殊的数据结构「单调栈」monotonic stack，解决了一类问题「Next Greater Number」，本文写一个类似的数据结构「单调队列」。

也许这种数据结构的名字你没听过，其实没啥难的，就是一个「队列」，只是使用了一点巧妙的方法，使得队列中的元素单调递增（或递减）。这个数据结构有什么用？可以解决滑动窗口的一系列问题。

看一道 LeetCode 题目，难度 hard：

特殊数据结构：单调队列 - 图1

一、搭建解题框架

这道题不复杂，难点在于如何在 O(1) 时间算出每个「窗口」中的最大值，使得整个算法在线性时间完成。在之前我们探讨过类似的场景，得到一个结论：

在一堆数字中，已知最值，如果给这堆数添加一个数，那么比较一下就可以很快算出最值；但如果减少一个数，就不一定能很快得到最值了，而要遍历所有数重新找最值。

回到这道题的场景，每个窗口前进的时候，要添加一个数同时减少一个数，所以想在 O(1) 的时间得出新的最值，就需要「单调队列」这种特殊的数据结构来辅助了。

一个普通的队列一定有这两个操作：

  1. class Queue {
  2.     void push(int n);
  3.     // 或 enqueue，在队尾加入元素 n
  4.     void pop();
  5.     // 或 dequeue，删除队头元素
  6. }

一个「单调队列」的操作也差不多：

  1. class MonotonicQueue {
  2.     // 在队尾添加元素 n
  3.     void push(int n);
  4.     // 返回当前队列中的最大值
  5.     int max();
  6.     // 队头元素如果是 n，删除它
  7.     void pop(int n);
  8. }

当然，这几个 API 的实现方法肯定跟一般的 Queue 不一样，不过我们暂且不管，而且认为这几个操作的时间复杂度都是 O(1)，先把这道「滑动窗口」问题的解答框架搭出来：

  1. vector<int> maxSlidingWindow(vector<int>& nums, int k) {
  2.     MonotonicQueue window;
  3.     vector<int> res;
  4.     for (int i = 0; i < nums.size(); i++) {
  5.         if (i < k - 1) { //先把窗口的前 k - 1 填满
  6.             window.push(nums[i]);
  7.         } else { // 窗口开始向前滑动
  8.             window.push(nums[i]);
  9.             res.push_back(window.max());
  10.             window.pop(nums[i - k + 1]);
  11.             // nums[i - k + 1] 就是窗口最后的元素
  12.         }
  13.     }
  14.     return res;
  15. }

图示

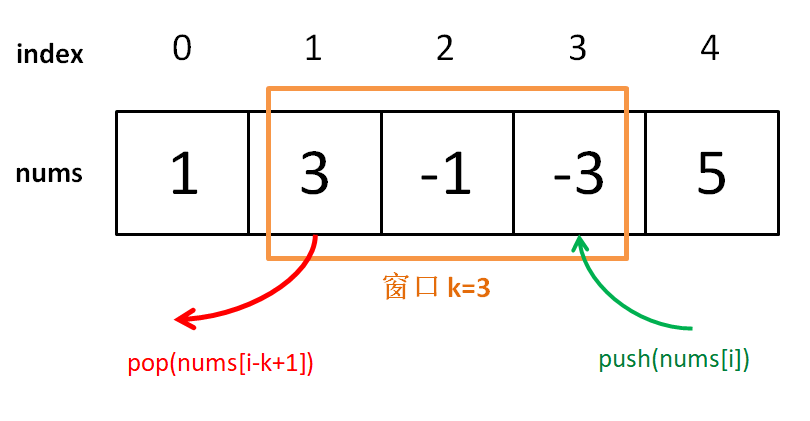
这个思路很简单，能理解吧？下面我们开始重头戏，单调队列的实现。

二、实现单调队列数据结构

首先我们要认识另一种数据结构：deque，即双端队列。很简单：

  1. class deque {
  2.     // 在队头插入元素 n
  3.     void push_front(int n);
  4.     // 在队尾插入元素 n
  5.     void push_back(int n);
  6.     // 在队头删除元素
  7.     void pop_front();
  8.     // 在队尾删除元素
  9.     void pop_back();
  10.     // 返回队头元素
  11.     int front();
  12.     // 返回队尾元素
  13.     int back();
  14. }

而且，这些操作的复杂度都是 O(1)。这其实不是啥稀奇的数据结构，用链表作为底层结构的话，很容易实现这些功能。

「单调队列」的核心思路和「单调栈」类似。单调队列的 push 方法依然在队尾添加元素，但是要把前面比新元素小的元素都删掉：

  1. class MonotonicQueue {
  2. private:
  3.     deque<int> data;
  4. public:
  5.     void push(int n) {
  6.         while (!data.empty() && data.back() < n) 
  7.             data.pop_back();
  8.         data.push_back(n);
  9.     }
  10. };

你可以想象，加入数字的大小代表人的体重，把前面体重不足的都压扁了，直到遇到更大的量级才停住。

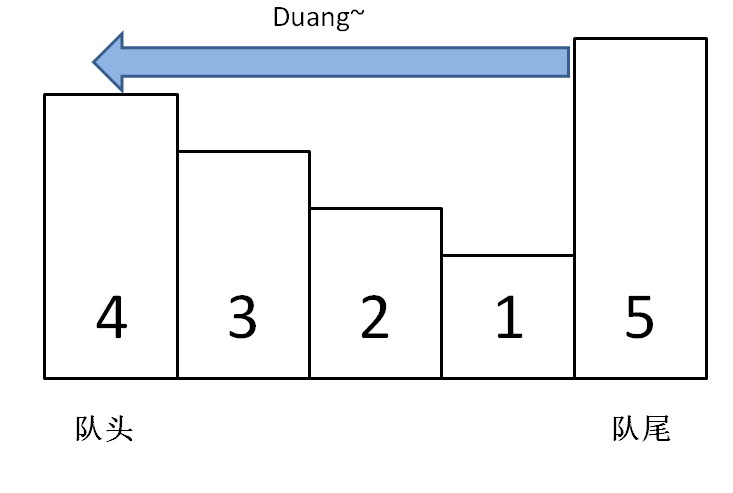
特殊数据结构：单调队列 - 图3

如果每个元素被加入时都这样操作，最终单调队列中的元素大小就会保持一个单调递减的顺序，因此我们的 max() API 可以可以这样写：

  1. int max() {
  2.     return data.front();
  3. }

pop() API 在队头删除元素 n，也很好写：

  1. void pop(int n) {
  2.     if (!data.empty() && data.front() == n)
  3.         data.pop_front();
  4. }

之所以要判断 data.front() == n，是因为我们想删除的队头元素 n 可能已经被「压扁」了，这时候就不用删除了：

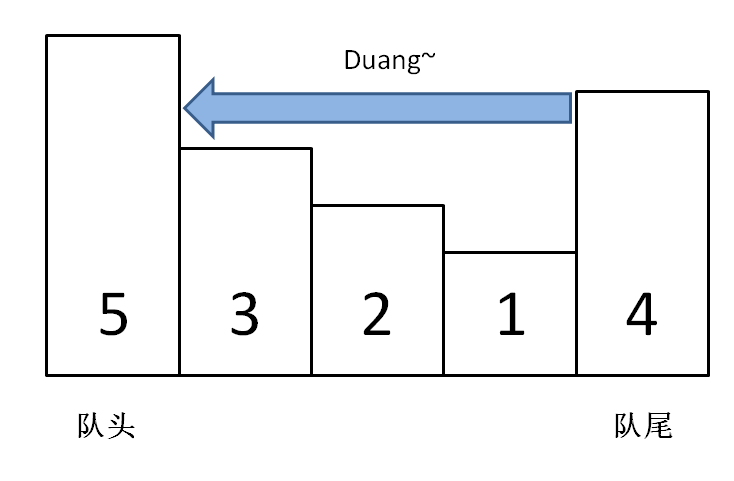
特殊数据结构：单调队列 - 图4

至此，单调队列设计完毕，看下完整的解题代码：

  1. class MonotonicQueue {
  2. private:
  3.     deque<int> data;
  4. public:
  5.     void push(int n) {
  6.         while (!data.empty() && data.back() < n) 
  7.             data.pop_back();
  8.         data.push_back(n);
  9.     }
  11.     int max() { return data.front(); }
  13.     void pop(int n) {
  14.         if (!data.empty() && data.front() == n)
  15.             data.pop_front();
  16.     }
  17. };
  19. vector<int> maxSlidingWindow(vector<int>& nums, int k) {
  20.     MonotonicQueue window;
  21.     vector<int> res;
  22.     for (int i = 0; i < nums.size(); i++) {
  23.         if (i < k - 1) { //先填满窗口的前 k - 1
  24.             window.push(nums[i]);
  25.         } else { // 窗口向前滑动
  26.             window.push(nums[i]);
  27.             res.push_back(window.max());
  28.             window.pop(nums[i - k + 1]);
  29.         }
  30.     }
  31.     return res;
  32. }

三、算法复杂度分析

读者可能疑惑，push 操作中含有 while 循环，时间复杂度不是 O(1) 呀，那么本算法的时间复杂度应该不是线性时间吧？

单独看 push 操作的复杂度确实不是 O(1)，但是算法整体的复杂度依然是 O(N) 线性时间。要这样想，nums 中的每个元素最多被 push_back 和 pop_back 一次，没有任何多余操作，所以整体的复杂度还是 O(N)。

空间复杂度就很简单了，就是窗口的大小 O(k)。

四、最后总结

有的读者可能觉得「单调队列」和「优先级队列」比较像，实际上差别很大的。

单调队列在添加元素的时候靠删除元素保持队列的单调性，相当于抽取出某个函数中单调递增（或递减）的部分；而优先级队列（二叉堆）相当于自动排序，差别大了去了。

赶紧去拿下 LeetCode 第 239 道题吧～