R 非线性最小二乘

当模拟真实世界数据用于回归分析时，我们观察到，很少情况下，模型的方程是给出线性图的线性方程。大多数时候，真实世界数据模型的方程涉及更高程度的数学函数，如3的指数或sin函数。在这种情况下，模型的图给出了曲线而不是线。线性和非线性回归的目的是调整模型参数的值，以找到最接近您的数据的线或曲线。在找到这些值时，我们将能够以良好的精确度估计响应变量。

在最小二乘回归中，我们建立了一个回归模型，其中来自回归曲线的不同点的垂直距离的平方和被最小化。我们通常从定义的模型开始，并假设系数的一些值。然后我们应用R语言的nls()函数获得更准确的值以及置信区间。

语法

在R语言中创建非线性最小二乘测试的基本语法

  1. nls(formula, data, start)

以下是所使用的参数的描述

  • formula是包括变量和参数的非线性模型公式。

  • data是用于计算公式中变量的数据框。

  • start是起始估计的命名列表或命名数字向量。

实例

我们将考虑一个假设其系数的初始值的非线性模型。 接下来，我们将看到这些假设值的置信区间是什么，以便我们可以判断这些值在模型中有多好。

所以让我们考虑下面的方程为这个目的

  1. a = b1*x^2+b2
  2. `

让我们假设初始系数为1和3，并将这些值拟合到nls()函数中。 

  1. xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
  2. yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)
  4. # Give the chart file a name.
  5. png(file = "nls.png")
  8. # Plot these values.
  9. plot(xvalues,yvalues)
  12. # Take the assumed values and fit into the model.
  13. model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))
  15. # Plot the chart with new data by fitting it to a prediction from 100 data points.
  16. new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
  17. lines(new.data$xvalues,predict(model,newdata = new.data))
  19. # Save the file.
  20. dev.off()
  22. # Get the sum of the squared residuals.
  23. print(sum(resid(model)^2))
  25. # Get the confidence intervals on the chosen values of the coefficients.
  26. print(confint(model))

当我们执行上面的代码，它产生以下结果：

  1. [1] 1.081935
  2. Waiting for profiling to be done...
  3.        2.5%    97.5%
  4. b1 1.137708 1.253135
  5. b2 1.497364 2.496484

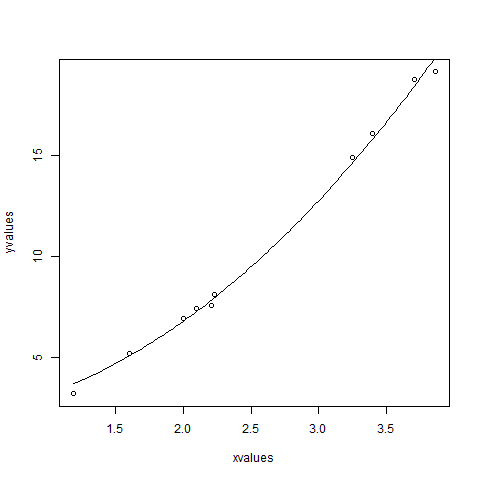
非线性至少方块R

我们可以得出结论，b1的值更接近1，而b2的值更接近2而不是3。